
Bienvenido. La semana pasada nos adentramos en el mundo del contraste de hipótesis, quizás con uno de los test estadísticos más intuitivos que existen, la prueba T (T-Test). Hoy continuaremos aprendiendo nuevos contrastes de hipótesis. Esta vez nos centraremos en las variables categóricas. Estas variables tienen un tratamiento algo especial cuando hablamos de contraste de hipótesis. Recuerda la tabla con la que terminábamos el post anterior, cuando nuestras variables son categóricas o categóricas y dummies (dicotómicas), usamos tablas de contingencia para llevar a cabo el contraste. Pero entonces ¿es suficiente con estas tablas? Simplificando la respuesta: no. La tabla nos da una idea de cómo los valores de dos variables se relacionan pero, como ocurría con el contraste de la semana anterior, no es suficiente con ver los datos, necesitamos aplicar alguna prueba estadística.
El contraste de hipótesis con variables categóricas
El objetivo de este contraste será determinar si dos variables se encuentran relacionadas mediante alguna medida de asociación, preferiblemente acompañada de su correspondiente prueba de significación. Es decir, primero comprobamos si se observa alguna asociación y luego tratamos de ver si ésta es estadísticamente significativa. Pero, para entender todo el proceso, es necesario hablar -siquiera brevemente- de las frecuencias que aparecen en las tablas que le pedimos a Stata con el comando tab.
Tablas de frecuencias y tablas de contingencia
Lo primero es distinguir entre tablas de frecuencia y tablas de contingencia. Como ya hemos mencionado previamente en este curso podemos pedir a Stata una tabla con la frecuencia con la que se repiten los valores de una variable (tabla de frecuencias) y también podemos pedirle una tabla en la que se cruzan las frecuencias de dos variables (tabla de contingencia) ambas se obtienen con el comando tab:
tab gol_est // tabla de frecuencias
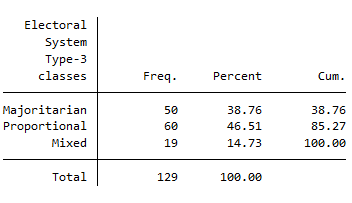
tab ht_region gol_est // tabla de contingencia
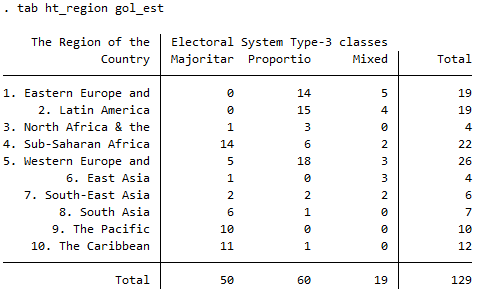
En la sesión anterior utilizábamos una única variable para comparar la media de dos grupos con la T-Test, a partir de ahora nos ceñiremos a las tablas de contingencia. Toda tabla de contingencia contiene frecuencias, marginales y, opcionalmente, porcentajes. Una pregunta pertinente antes de nada es saber que variable colocar en las filas y cuál en las columnas. No es en ningún caso obligatorio pero sí que se suele usar la convención de colocar en las columnas la variable independiente mientras que en las filas se coloca la variable dependiente. Así, en el siguiente ejemplo vemos el efecto de la región a la que pertenece el país (en columnas) sobre el tipo de sistema electoral del mismo (en filas):
tab gol_est ht_region

Para ver un poco más claras las partes de las que hablábamos, a continuación vemos las filas y las columnas transpuestas:

Para obtener los porcentajes se añade al comando tab una opción. Es posible pedir porcentajes “de fila” o “de columna”. Esto es relevante porque la interpretación de los porcentajes es distinta en cada caso. Si seguimos la convención de colocar en columnas la variable independiente, obtener los porcentajes por columna nos permite interpretar el efecto que esta variable explicativa tiene sobre la dependiente (será lo más común).
tab gol_est ht_region, column
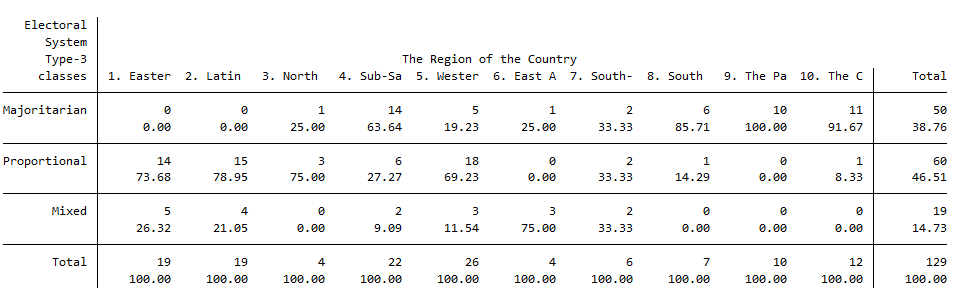
Fíjate que debajo de todos los marginales de columna ahora hay un 100, que indica que los porcentajes de cada columna suman esta cantidad. Por tanto, la interpretación sería:
De los países de la región “Latinoamérica” (segunda columna), un 78.95% tienen sistemas proporcionales, mientras que un 21.05% tienen sistemas mixtos.
La opción para obtener los porcentajes “de fila” es row. Y una manera de limpiar un poco la tabla para leer sólo porcentajes es indicarle a Stata que además de mostrar los porcentajes, elimine (no muestre) las frecuencias:
tab gol_est ht_region, col nofreq

¿Cómo calcula Stata los porcentajes?
Si llamamos \(f_{ij}\) a la frecuencia de la fila i y la columna j y \(f_i\) al marginal de la fila i, el porcentaje de la fila i y la columna j se calcula como el cociente entre las frecuencias y marginales de cada fila multiplicado por 100, es decir:
\[p_{ij}^H = \frac{f_{ij}}{f_i}\cdot100\]Para el caso de los porcentajes de columna, se usan los marginales de columna:
\[p_{ij}^V = \frac{f_{ij}}{f_j}\cdot100\]También existe la posibilidad de pedirle a Stata los porcentajes de “celda” pero su interpretación es más complicada y no haremos hincapié aquí.
Se calculan como sigue:
\[p_{ij}^T = \frac{f_{ij}}{f}\cdot100\]Y se piden en Stata así:
tab gol_est ht_region, cell
Finalmente, ¿cómo deben interpretarse (leerse) las tablas de contingencia con porcentajes? Siguiendo la regla de Zeisel:
Los porcentajes han de calcularse en la dirección de la variable independiente e interpretarse en la de la dependiente. Es decir, se calcularán porcentajes sobre la columna que habrán de ser interpretados por filas.
Para leer una tabla, por tanto, aplicaremos la Regla de Zeisel. Los porcentajes estarán calculados en columnas (variable independiente) y se compararán/interpretarán según filas (variable dependiente).
Esta comparación entre los porcentajes de columna y marginales sirve como primera aproximación al concepto de independencia de las tablas de contingencia Como veremos, parte de los estadísticos de significación y asociación estadística se basan en la comparación entre las frecuencias observadas de las casillas y las frecuencias esperadas.
Pues bien, estas frecuencias que aparecen por defecto con el comando tab se denominan frecuencias observadas, pues son las que se observan en la muestra con la que estamos trabajando, es decir, en los datos que estamos manejando. Sin embargo, podemos pedirle a Stata que nos muestre lo que se denominan frecuencias esperadas, es decir, las frecuencias teóricas que esperaríamos en el hipotético caso de que las variables que hemos enfrentado en la tabla de contingencia no tuvieran ninguna relación entre sí.
Medidas de asociación y significación
Para calcular las frecuencias esperadas \(f_{ij}^*\) Stata utiliza la siguiente fórmula:
\[f_{ij}^* = \frac{f_if_j}{f_{..}}\]donde \(f_i\) es el total de fila, \(f_j\) el total de columna y \(f_{..}\) el número total de casos. Veamos un ejemplo:
Sea la siguiente tabla de contingencia:
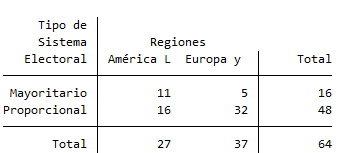
Para calcular la tabla teórica, es decir, las frecuencias esperadas, usamos las fórmulas de arriba:
La frecuencia esperada en la fila 1, columna 1 (\(f_{11}\)), es decir, la cantidad esperada de países de América Latina y el Caribe con sistema electoral mayoritario (si no hubiera ningún efecto de la región geográfica sobre el tipo de sistema electoral) sería:
\[f_{11} = \frac{f_1\cdot f_1}{f_{..}} = \frac{16\cdot27}{64} = 6.75\]Y así sucesivamente. Finalmente obtendríamos la tabla teórica que -por supuesto- no vamos a calcular a mano, y en Stata puede obtenerse de la siguiente forma:
tab sis_elec regiones, expected //Esto muestra tanto las observadas como las esperadas
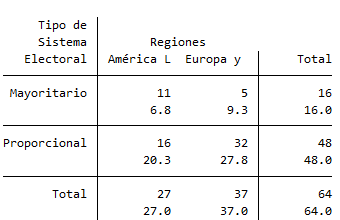
Así, podemos comparar los valores observados con los esperados. Pues bien, el hecho de que la tabla observada no sea idéntica a la teórica nos indica que estas variables tienen algún tipo de asociación, es decir, que la variable independiente tiene cierto efecto sobre la variable dependiente. Una primera forma de ver qué tipo de efecto consiste en obtener los residuos.
Los residuos son las diferencias existentes en cada casilla entre la tabla empírica y la tabla teórica, es decir, entre las frecuencias observadas y las frecuencias esperadas (esperadas si no hubiera relación entre las variables) (Martín, 2008)
Por tanto los residuos se calculan de la siguiente manera:
\[r_{ij} = f_{ij}-f_{ij}^\prime\]Ahora bien, suele ser más interesante utilizar estos residuos tipificados. Estos se llaman residuos de Pearson o estandarizados y no son más que el residuo neto dividido por la raíz cuadrada de la frecuencia esperada:
\[r_{ij}^S = \frac{f_{ij}-f_{ij}^\prime}{\sqrt{f_{ij}^\prime}}\]Finalmente, una forma más refinada aún de mostrar los residuos es obtener los residuos corregidos o ajustados a través de la siguiente fórmula:
\[r_{ij}^A = \frac{r_{ij}^S}{\sqrt{(1-\frac{f_i}{f})\cdot(1-\frac{f_j}{f}))}}\]Para obtener la tabla de residuos de Pearson o los residuos ajustados en Stata es necesario instalar un paquete (.ado). Los paquetes .ado son comandos que extienden la funcionalidad de Stata. Son comandos escritos por la comunidad y pueden instalarse con el comando ssc install. Para obtener los residuos ajustados y de Pearson en concreto necesitamos el comando tabchi:
ssc install tab_chi
Ahora, ya podemos pedir a Stata cualquier tipo de residuo.
tabchi sis_elec regiones, raw pearson adjust noo noe
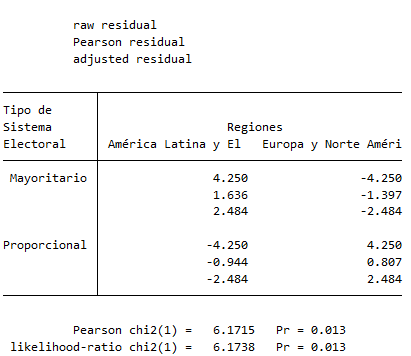
Como ves, arriba Stata nos indica que en cada celda de la tabla se puede leer el residuo “crudo”, a continuación el residuo de Pearson y finalmente el residuo ajustado. Cada uno de ellos se obtiene con una de las opciones tras la coma en el código de arriba, así que usa el que más te convenga en cada caso. Las opciones noo y noe son para pedirle a Stata que no muestre las frecuencias observadas ni las esperadas.
Como podrás haber intuido los residuos pueden tener signo, pues el valor observado puede ser mayor o menor que el esperado. Un residuo positivo indica que el valor observado es mayor que el esperado mientras que un residuo negativo indica que el valor observado es menor que el esperado. Esto ya nos da una idea de la dirección de la relación entre las variables.
En general, si el residuo ajustado supera \(1.96\) en términos absolutos (negativo o positivo) puede decirse que la diferencia entre el valor observado y el esperado en caso de no haber relación entre las variables no es debido al azar con un 95% de confianza.
Esto es muy útil, pues nos permite saber específicamente en qué casillas se da una relación estadísticamente significativa entre las variables. Sin embargo, para tener una medida que nos permita contrastar una hipótesis, aún nos queda hablar de las dos últimas líneas de esta salida.
La Chi-cuadrado y la razón de verosimilitud
Además de la significación de cada casilla, es posible medir si la relación global entre las dos variables es significativa. Para esto se utilza el estadístico chi-cuadrado o ji-cuadrado(\(\chi^2\))
Este estadístico fue propuesto por Pearson y permite contrastar la hipótesis de que los dos criterios de clasificación utilizados (las dos variables categóricas) son independientes. Es decir, se parte de la hipótesis nula de independencia de las variables. Para el que esté interesado, el estadístico se construye a partir de las frecuencias esperadas para cada casilla siguiendo la siguiente fórmula:
\[\chi^2=\sum^m_{j=1}\sum^n_{i=1} \frac{(f_{ij}-f_{ij}^\prime)}{f_{ij}^\prime}\]Por tanto, simplemente es la suma de los residuos tipificados al cuadrado (veremos esto con más detalle cuando hablemos del modelo de regresión lineal simple).
Lo más importante es recordar que este estadístico vale cero cuando las variables son completamente independientes. Asimismo, es mayor cuanto mayor sea la discrepancia entre las \(f_o\) y las \(f_e\) (o cuanto mayor sea la relación entre las variables).
ATENCIÓN: Sin embargo, este estadístico no suele utilizarse como indicador de la fuerza de la asociación porque no está estandarizado entre 0 y 1. Veremos más abajo qué estadísticos usar para este propósito.
El estadístico \(\chi^2\) sigue una distribución conocida según sus Grados de Libertad que se pueden obtener como sigue:
\[gl=(k-1)\cdot(r-1)\]donde \(k\) es el número de filas en la tabla y \(r\) es el número de columnas. La representación gráfica de este estadístico es la siguiente:

Al no ser este un curso de estadística, no entraremos en más detalles sobre el estadístico y sus grados de libertad. Para calcular el valor del estadístico debe usarse la fórmula de arriba. Sin embargo, Stata calcula por nosotros este valor como podemos leer en la última salida del apartado anterior. En ese caso, estamos ante una \(\chi^2\) con 1 grado de libertad (entre paréntesis) que tiene un valor de \(6.1715\). Pero el valor en el que debemos fijarnos para el contraste de hipótesis es el que está al lado, de nuevo, el famoso p-value (\(Pr=0.013\)).
Si el p-value se encuentra por debajo de 0.05, es decir, el valor de \(\alpha\), diremos que hay evidencia suficiente en contra de la hipótesis nula de independencia y, por tanto, podemos concluir que las variables enfrentadas están relacionadas y que esta asociación es estadísticamente significativa con un nivel de confianza del 95%.
Por tanto, en nuestro ejemplo, la región y el tipo de sistema electoral están asociados y esta relación es estadísticamente significativa con una confianza del 95%.
La segunda fila de la salida que estamos analizando indica la razón de verosimilitud, que se basa en el cociente de las diferencias entre las frecuencias observadas y esperadas en lugar de en su diferencia, como podemos ver en la siguiente fórmula:
\[L^2 = 2\sum^m_{j=1}\sum^n_{i=1}f_{ij}\ln{\frac{f_{ij}}{f_{ij^*}}}\]Simplemente se trata de otra alternativa para testar la hipótesis nula de independencia que es especialmente útil cuando los valores de las frecuencias esperadas son muy pequeñas (menores que 5). En tales casos, los valores de la razón de verosimilitud y de la \(\chi^2\) difieren (y el primero es más preciso), pero tienden a converger cuando los valores de las frecuencias esperadas aumentan.
El estadístico exacto de Fischer
Ofrece la probabilidad exacta de obtener las frecuencias de hecho obtenidas o cualquier otra combinación más alejada de la hipótesis de independencia. Es utilizado principalmente para muestras pequeñas y tablas con dos variables dicotómicas (2x2).
Sin embargo, estos estadísticos sólo nos dan una idea de la existencia de relación pero no de su fuerza. Para saber si una relación es fuerte o débil entre variables éstos no son suficientes. Para ello recurrimos a los estadísticos de asociación.
Las medidas de asociación
Existen distintas medidas de asociación. Para elegir una medida concreta es necesario conocer las características particulares de cada medida, así como el tipo de variables estudiadas y la hipótesis que queremos contrastar.
En ningún caso está justificado obtener todas las medidas disponibles para seleccionar aquélla cuyo valor se ajusta a nuestros intereses. (Pinta 2020)
Medidas nominales de asociación
Estas medidas se emplean para variables nominales (cualitativas). Y es importante recordar que sólo informan del grado de asociación existente, no de la dirección de la asociación. En general se basan en la chi-cuadrado y sirven para corregir su valor estandarizándolo entre 0 y 1. Entre ellas se encuentran:
- El coeficiente Phi (\(\phi\)): es una medida del grado de asociación entre dos variables dicotómicas (2x2) basada en el estadístico \(\chi^2\) (Ferrán, 2001) y que toma valores entre 0 y 1 (0 indicará ninguna asociación y valores cercanos a 1 asociación fuerte).
- El Coeficiente de Contingencia (C): Es una extensión de Phi para tablas mayores de 2x2. Toma valores en el intervalo [0,1), es decir, no alcanza el 1. Su expresión es: \(C=\sqrt{\frac{\chi^2}{\chi^2+n}}\)
De nuevo, \(C=0\) indica independencia mientras que \(C=C_{max}\) indica fuerte asociación. El mayor problema que tiene este coeficiente es que no sirve para comparar tablas de dimensiones distintas porque su cota máxima depende de las dimensiones de la tabla de contingencia.
- Para solucionar las deficiencias del Coeficiente de contingencia se usa la V de Cramer que está normalizado entre 0 y 1. Una vez más, valores cercanos a 0 indican no asociación mientras que valores próximos a 1 asociación fuerte. Su expresión es la siguiente:
La V de Cramer, entonces, se usa para variables nominales de más de dos categorías
Medidas ordinales de asociación
Como su nombre indica, utiliza variables ordinales y, al poder ordenarse sus valores, estas medidas nos sirven para conocer tanto la fuerza de la asociación como la dirección de la relación. Resumiendo:
- Una relación positiva indica que los valores altos de una variable se asocian con valores altos de otra, y los valores bajos, con los valores bajos.
- Una relación negativa indica que los valores altos de una variable se asocian con valores bajos de la otra, y los valores bajos con los valores altos.
Para estudiar la relación entre variables ordinales estas medidas están basadas en el concepto de inversión y no inversión realizando un cálculo de los pares posibles de valores. Es decir:
- Si los valores de un caso en ambas variables son mayores (o menores) que los dos valores de otro caso, decimos que entre esos casos se da una no inversión (concordantes) (P o C).
- Si el valor de un caso en una de las variables es mayor que el de otro caso, y en la otra variable el valor del segundo caso es mayor que el del primero, decimos que se da una inversión (discordantes) (Q o D).
- Si dos casos tienen valores idénticos en una o en las dos variables, decimos que se da un empate (E).
Entonces:
- Cuando predominan las no inversiones , la relación es positiva: conforme aumentan (o disminuyen) los valores de las variables, aumentan (o disminuyen) los de la otra.
- Cuando predominan las inversiones, la relación es negativa: conforme aumentan (o disminuyen) los valores de una de las variables, disminuyen (o aumentan) los de la otra.
Fuente: De la Fuente Fernández, 2011
Uno de los coeficientes más famosos es el Coeficiente Gamma:
\[\gamma=\frac{P-Q}{P+Q}\]Donde \(P\) son los pares concordantes y \(Q\) los pares discordantes.
Básicamente, \(\gamma\) cuenta, para cada casilla, el número total de pares de casos concordantes y discordantes para medir la relación entre ambas variables.
Este coeficiente, a diferencia de los anteriores oscila entre -1 y 1, por lo que:
- Si la relación entre dos variables es perfecta y positiva: \(\gamma = 1\)
- Si la relación entre las variables es perfecta y negativa: \(\gamma = -1\)
- Si las variables son independientes: \(\gamma = 0\)
Tau-b de Kendall y Tau-c de Kendall
Existen otros dos estadísticos parecidos al coeficiente Gamma, las Tau (\(\tau\)) de Kendall. la primera o Tau-b (\(\tau_b\)) incorpora una corrección del coeficiente Gamma en el denominador, por lo que es un estadístico más “conservador” que Gamma. Sólo puede usarse en tablas cuadradas y su expresión es la siguiente:
\[\tau_b = \frac{P-Q}{\sqrt{(P+Q+T_X)(P+Q+T_Y)}}\]A su vez, la Tau-c (\(\tau_c\)) no es sino una corrección de la Tau-b para tablas rectangulares. Es de mencionar que este estadístico tiende a subestimar el verdadero grado de asociación entre las variables (Ferrán, 2001:64-65).
\[\tau_c = \frac{2\min(I,J)(P-Q)}{n^2 \min(I-1,J-1)}\]Si la tabla es cuadrada, las Tau de Kendall son prácticamente iguales.
Un resumen de las medidas de asociación y significación
| Variables cruzadas | Número de categorías | Medida de asociación | Indicación de dirección |
|---|---|---|---|
| Nominal X Nominal | Solo (2x2) | Phi | Sí |
| Nominal X Nominal | Mayor de (2x2) | V de Cramer | No |
| Nominal X Ordinal | Al menos (2x3) | V de Cramer | No |
| Ordinal X Ordinal | Cuadrada (ej. 3x3) | Tau-b de Kendall | Sí |
| Ordinal X Ordinal | Rectangular (ej. 3x4) | Tau-c de Kendall | Sí |
| De intervalo X De intervalo | R de Pearson | Sí |
Fuente: Adaptado de Data Art
Todos estos estadísticos se pueden pedir en Stata con el comando tab.
tabulate variable1 variable2, chi2 lrchi2 exact V gamma taub [all] [nofreq] [col] [row] // Con la opción "all" Stata calcula todos los estadísticos indicados arriba
Construcción de índices
Para terminar este post, veremos qué es y cómo se construye un índice. Esto nos será muy útil para las sesiones venideras y para tu trabajo.
¿Qué es un índice?
Supongamos que se desee evaluar el comportamiento de una variable para la cual, una vez elaboradas las definiciones correspondientes, se hayan encontrado diversos indicadores capaces de expresar los valores que asume en distintos objetos. A través de cada indicador, se podrán obtener los datos pertinentes, que deberán ser llevados a escalas adecuadas para ordenarlos. Para cada indicador que utilicemos, será necesario adoptar o construir una escala que cuantifique las observaciones realizadas. De acuerdo con los datos obtenidos, evaluaremos en cada escala el comportamiento que sigue cada indicador. No obstante, esto no nos permite todavía medir claramente la variable, pues nos entrega información fragmentaria, que debe ser integrada o sintetizada para llegar a un valor único, que exprese lo que en realidad ocurre con la variable. Para lograrlo, debemos sumar ponderadamente los valores de los indicadores, obteniendo un valor total que se denomina índice, y que es el que nos dará la información relevante sobre el problema en estudio.
Para construir un índice, por tanto, necesitamos varias variables de la base de datos que sirvan para medir una misma característica. En el caso de Quality of Government, por ejemplo, hay tres variables de calidad de la burocracia: qs_close, qs_impar, qs_proff. Lo primero que debemos hacer es examinar las correlaciones entre estas variables (veremos más sobre correlación en la próxima sesión):
corr qs_closed qs_impar qs_proff pwcorr qs_closed qs_impar qs_proff, obs sig // Con la opción obs pido las observaciones para cada cruce y con la opción sig pido la significación estadística. // Buscamos aquella (o aquellas) relaciones estadísticamente significativas, es decir, con un p-value inferior a 0.05
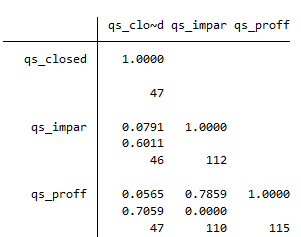
Vemos que la pareja qs_proff y qs_impar tienen una correlación de 0.786 (más sobre esto en la siguiente sesión) y un p-value de prácticamente 0 así que se pueden combinar para crear un índice. Lo hacemos de la siguiente manera:
gen bureaucracy=(qs_impar + qs_proff)/2 // Suma ponderada (una media de los valores) sum bureaucracy // Si queréis comprobar cómo queda
Ya tienes un índice que mide la burocracia usando dos indicadores listo para usarlo.
Si has llegado hasta aquí, enhorabuena, ha sido un post duro y con mucha información. En la próxima sesión veremos el último contraste de hipótesis previo al modelo de regresión (el ANOVA) y nos adentraremos en el mundo de la correlación.