Bienvenido/a una semana más. Hasta ahora hemos visto cómo limpiar los datos y prepararlos para trabajar, cómo formular una hipótesis científica y algunos métodos estadísticos para ponerlas a prueba empíricamente. Especialmente hemos hablado de la prueba T para comparar las medias de dos grupos y los estadísticos de asociación y significación típicos del contraste de hipótesis para variables categóricas (usando para ello tablas de contingencia). Esta semana ampliaremos la prueba T para el caso en el que tengamos que comparar la media de una variable continua entre más de dos grupos. Para ello usaremos el Análisis de Varianza (ANOVA por sus siglas en inglés). Asimismo, introduciremos el concepto de correlación para encaminarnos al último punto del curso, el modelo de regresión lineal simple.
El Análisis de Varianza (ANOVA)
Cuando uno necesita comparar los valores medios de una variable dependiente continua según las categorías de otra variable normalmente utiliza una T-Test, como hemos visto ya en el curso. Sin embargo, esta prueba sólo sirve si la variable independiente de agrupación es dicotómica. En realidad lo que hacemos con una T-Test es comparar la media de dos muestras o la media de dos grupos de la muestra. Sin embargo, son muchos los casos en los que encontraremos una característica que queramos analizar comparando no sólo dos, sino más grupos. Para esto se usa el análisis de varianza (ANOVA). En realidad, el ANOVA no es más que una generalización del contraste de medias para dos muestras, aplicable a situaciones en las que en lugar de dos, sean TRES O MÁS las muestras o grupos de que disponemos. Se suele hablar de ANOVA de un factor. Se denomina factor a la variable independiente, es decir, a la variable categórica de agrupación (sea esta nominal u ordinal). Por contra, la variable dependiente debe ser continua (de intervalo o de razón).
Recuerda que siempre que se hace un contraste de hipótesis es necesario saber de qué hipótesis nula se parte. Si recuerdas, en la prueba T se parte de la suposición de que no existe diferencia entre las medias de los grupos comparados. Es decir:
\[H_0: \mu_1-\mu_2 = 0\] \[H_0: \mu_1=\mu_2\]Pues bien, en el caso del ANOVA, la hipótesis nula que se pone a prueba es que las medias poblacionales (las medias de la VD en cada nivel de la VI) son iguales. Es decir, la misma hipótesis nula que para la prueba T pero con más de dos niveles en la variable independiente:
\[H_0: \mu_1=\mu_2 =\mu_3=...=\mu_k\; k \in{\mathbb{N}}\]Para poner a prueba esta hipótesis se utiliza un estadístico llamado F, cuya distribución de probabilidad es conocida. De hecho, si las poblaciones son normales y sus varianzas son iguales, el estadístico F se distribuye según el modelo de probabilidad F de Fischer-Snedecor y se interpreta de manera similar al estadístico T de Student para la prueba T. Por si a alguien le interesa la construcción matemática de este estadístico, ésta consiste en el cociente entre dos estimadores diferentes de la varianza poblacional:
- El numerador es una estimación de la varianza poblacional basada en la variabilidad existente entre las medias de cada grupo.
- El denominador es también una estimación de la varianza poblacional, pero basada en la variabilidad existente dentro de cada grupo.
donde MCE es la media cuadrática externa (intergrupal)
\[MCE=\frac{SCE}{k-1}\]y MCI es la media cuadrática interna (intragrupal)
\[MCE=\frac{SCI}{n-k}\]donde \(k\) es el número de grupos de la variable independiente y \(n\) el número total de observaciones.
En definitiva, los modelos ANOVA analizan qué porcentaje de la varianza de una variable cuantitativa puede ser explicado por la pertenencia a diferentes grupos de una variable cualitativa. Por ello se divide la varianza inter-grupos por la varianza intra-grupos. Cuando mayor es este cociente, más intensa es la relación entre las dos variables. Como siempre, si el nivel crítico asociado a F es menor que 0.05, rechazaremos la hipótesis de igualdad de medias y concluiremos que no todas las medias poblacionales comparadas son iguales.
Para pedir a Stata que aplique el Análisis de Varianza (ANOVA) de un factor usamos el comando oneway:
oneway variable variableagrupación [,tabulate scheffe bonferoni noanova] // tabulate sirve para obtener una tabla resumen // scheffe y bonferroni son pruebas de comparaciones múltiples que veremos enseguida // y noanova suprime la tabla de ANOVA
Para llevar a cabo el ANOVA partimos de los siguientes supuestos:
- Las muestras se han seleccionado aleatoria e independientemente de las k poblaciones
- Las distribuciones en la población de la variable dependiente (de la que se calcula la media) son normales en cada uno de los grupos
- Las desviaciones típicas de la variable en cada una de las poblaciones son iguales entre sí
Existen pruebas tanto para la condición segunda (normalidad) como para la tercera (homocedasticidad), pero no es necesario ir tan lejos en este nivel. Si a alguien le interesa, es habitual usar la prueba de Shapiro-Wilk para normalidad (en Stata es el comando swilk) y para comprobar la homocedasticidad se usa el test de Levene (en Stata el comando es robvar).
Veamos un ejemplo:
oneway cspf_sfi orig_col // La variable orig_col es una recodificación de ht_region (el origen colonial del país)
Resultado:

En esta salida vemos una tabla con varios números importantes:
La suma cuadrática total (Total SS o SCT): suma de las desviaciones al cuadrado de todos los valores respecto a la media global de la muestra. No es otra cosa que el numerador de la varianza, por lo que al dividirla por los grados de libertad de la muestra (gl o df), se obtiene la cuasivarianza, conocida en este contexto como la media cuadrática total (Total MS o MCT)
\[SCT = \sum_{j=1}^{k}\sum_{i=1}^{n_j}(x_{ij-\bar{x}})^2\] \[MCT = \frac{SCT}{n-1}\]Esta suma cuadrática se descompone en dos: intergrupal (between groups) e intragrupal (within groups). La primera recoge las desviaciones al cuadrado de cada una de las medias de los grupos respecto a la media global, mientras que la segunda representa las desviaciones de los valores con respecto a la media de su grupo (Escobar et al.(2009:219)). Es decir, observamos la variación existente entre las medias de los grupos (variación inter-grupos) y la variación existente entre las puntuaciones dentro de cada grupo (variación intra-grupos). Las medias cuadráticas no son más que el resultado de dividir estas sumas de cuadrados entre sus correspondientes grados de libertad.
Así, dividiendo las medias cuadráticas intergrupal e intragrupal se obtiene el valor del estadístico F, pues recuerda que este cociente sigue la distribución F de Fischer-Snedecor si se cumplen ciertas condiciones. Por tanto, cuando mayor sea el valor del estadístico F, más probable será que existan diferencias significativas entre los grupos. Para interpretar mejor este valor de F, como siempre, se usa su p-value asociado que, cuanto más bajo sea, más evidencia arrojará contra la hipótesis nula de igualdad de medias.
Sin embargo, esta tabla y este análisis no es suficiente para decir algo sobre la potencial relación existente entre la variable dependiente y la independiente. Sólo sabemos hasta ahora que existe evidencia contra la hipótesis de igualdad de medias, es decir que éstas difieren, pero ¿son diferentes entre sí todas las medias?, ¿hay sólo una media que difiere de las demás?
Para resolver esta cuestión usamos una de las dos pruebas de comparaciones múltiples que pueden llevarse a cabo en Stata (Scheffe o Bonferroni). Son muy similares, así que optaremos por una de ellas exclusivamente.
oneway cspf_sfi orig_col, noanova scheffe // Evito que vuelva a salir la tabla del ANOVA con la opción noanova
Resultado:

El resultado es una tabla con los cruces dos a dos de las categorías de la variable independiente. Vemos que sólo los cruces entre franceses-españoles y británicos-españoles son significativos (p-value inferior a alfa). es decir, que no hay una diferencia estadísticamente significativa entre la media de fragilidad del Estado de los países colonizados por franceses y británicos pero si entre estos dos con respecto a los países colonizados por los españoles. Si volvemos a mirar la tabla del ANOVA, veremos que la fragilidad es mayor en países colonizados por los británicos y mayor aún en aquellos colonizados por los franceses.
Para terminar esta sección, si quisieras hacer un análisis de varianza de más de un factor, debes usar el comando anova en lugar de oneway. Sin embargo, no haremos hincapié en esta posibilidad porque el resultado de este tipo de análisis es prácticamente idéntico al del modelo de regresión lineal que veremos en la próxima sesión.
Covarianza y Correlación
Cuando hablamos de covarianza o correlación nos referimos a variables cuantitativas, es decir, numéricas y (normalmente) continuas (Ej. PIB per cápita, gasto militar, nivel de ingresos…). Pues bien, se considera que dos variables cuantitativas están relacionadas entre sí cuando los valores de una de ellas varían de forma sistemática con respecto a los valores de la otra. Esto es similar a lo que veíamos en la sesión anterior para variables categóricas y tablas de contingencia. Así que ahora nos centraremos en estudiar la asociación pero entre variables cuantitativas. Dicho en otros términos, si consideramos dos variables X e Y, existe relación entre ellas si al aumentar los valores de X también lo hacen los de Y, o por el contrario, si al aumentar los valores de X, disminuyen los de Y.
Si recuerdas la sesión sobre gráficos en Stata, para el caso de dos variables cuantitativas continuas era habitual usar el diagrama de dispersión o nube de puntos, (scatter plot en inglés). Es la forma más intuitiva de ver si dos variables están relacionadas. Sin embargo, esta relación puede adoptar distintas formas:
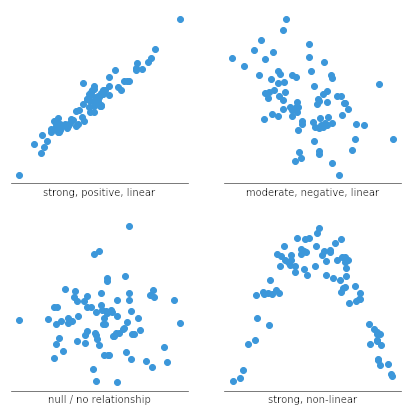
Siempre se representa en el eje de abscisas (horizontal) la variable independiente o predictora (X) y en el eje de ordenadas (vertical) la dependiente o resultado (Y). En el interior del gráfico se representa un punto por cada observación, es decir, un par de valores (coordenadas) X,Y. Por tanto, estos gráficos nos sirven para ver una aproximación a la relación entre las variables. Estas relaciones pueden ser clasificarse atendiendo, al menos, a tres criterios:
- La fuerza: la relación será más fuerte cuanto más alineados estén los puntos
- El sentido: la relación puede ser positiva o negativa según los cambios en una de las variables hagan cambiar en la misma dirección a en la contraria a la otra.
- La forma: la relación podrá ser lineal (la nube de puntos tenderá a tener forma de recta), cuadrática (una parábola), logarítmica, etc.
En definitiva, lo que vemos en este tipo de gráficos es hasta qué punto sucede que la variación de una variable sucede a la vez que la variación de la otra. Es decir, si estas dos variables covarían. Es por esto que se habla de covarianza.
La covarianza nos sirve para comprender la asociación entre dos variables cuantitativas. Indica el grado de variación conjunta de dos variables respecto a sus medias. Como puede intuirse, procede del concepto de varianza que, recuerda, mide la dispersión de una variable, es decir, la distancia media de sus valores con respecto a su media. Pues en el caso de trabajar con dos variables, se pueden calcular sendas distancias con respecto a las respectivas medias, una para cada variable.
\[(x_i-\bar{x})(y_i-\bar{y})\]Pues bien, la covarianza es un promedio del producto entre estas dos distancias, y su fórmula adopta la siguiente expresión:
\[S_{xy} = Cov(X,Y) = \frac{\sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y})f_i}{\sum_{i=1}^{n}f_i}\]La covarianza nos informa del sentido de la relación pero no de la intensidad o fortaleza de ésta. Puede ser positiva y negativa, y el signo nos señala si la nube de puntos es creciente o decreciente pero no nos dice nada sobre el grado/intensidad de la relación entre las variables. Además, no está acotada, es decir, depende de la escala de medida. Lo que podemos concluir, por tanto, si nos fijamos en la fórmula de arriba es que si los valores de la variable \(x\) están por encima de su media (\(x_i>\bar{x}\)), esta parte de la multiplicación será positiva y negativa en caso contrario; y lo mismo se puede decir de los valores de \(y\) con respecto de su media. Por tanto, el signo de la covarianza será el signo de este producto, esto es, la covarianza será positiva cuando las dos variables se mueven en el mismo sentido y negativa cuando se mueven en sentido contrario.
Para resolver los problemas que plantea el hecho de que la covarianza no esté acotada ni normalizada, se utiliza el concepto de correlación. La corelación entre dos variables cuantitativas informa del sentido y la intensidad de la relación entre ellas, y se calcula dividiendo su covarianza por el cproducto de las desviaciones estándar de cada una. Al ser estas positivas, su signo es, por construcción, el mismo que el de la covarianza y se interpreta análogamente (Santana y Rama, 2017:72). A la correlación se le suele dar el nombre más técnico de coeficiente de correlación lineal de Pearson, y se denota normalmente con la letra griega \(\rho\). Es el estadístico que nos permite medir el sentido y fuerza de la relación lineal entre dos variables cuantitativas:
\[\rho_{xy}=\frac{Cov(X,Y)}{\sigma_x\sigma_y}\]o a veces también:
\[r = \frac{S_{xy}}{S_xS_y}\]De entre todos los tipos de relaciones expuestas más arriba, lo que en ciencias sociales suele interesarnos más (sobre todo de cara a la siguiente sesión) son las relaciones lineales. Buscamos, por tanto, nubes de puntos que se distribuyen en forma de recta, creciente o decreciente. Si ocurre esto, diremos que existe una relación lineal positiva (creciente) o negativa (decreciente) o también que existe correlación entre las variables. Sin embargo, la nube de puntos, esto es, la representación gráfica no es suficiente para saber la magnitud de la relación de manera precisa. Para ello utilizamos el estadístico mencionado, \(\rho\)
A diferencia de la covarianza, el coeficiente de correlación de Pearson \(\rho\) es INDEPENDIENTE DE LA ESCALA DE MEDICIÓN La correlación es, por tanto, ADIMENSIONAL y, al no depender de la escala de las variables, su magnitud informa objetivamente sobre la intensidad de la variación conjunta (o disjunta) de las variables (Sánchez Carrión, 1995 239 en Santana y Rama, 2017 72).
Este estadístico está acotado entre -1 (correlación perfecta de sentido negativo) y 1 (correlación perfecta de sentido positivo). Cuanto más cerca de 1 esté su valor absoluto más intensa es la relación entre las variables. Cuanto más cercano a 0 sea este valor, menor será la fuerza de la relación, indicando en ocasiones la ausencia de correlación entre las dos variables.
Sin embargo, hasta ahora hemos hablado de la relación entre dos vairables. Esto se debe a que el coeficiente de correlación de Pearson solo permite calcular un valor por cada par de variables, sin embargo, no es difícil obtener una matriz de correlaciones entre todos los pares potenciales de variables, como hicimos -si recuerdas- en la sesión anterior para crear un índice. En estas matrices, la diagonal principal siempre tiene como valor 1 ya que la correlación de una variable con ella misma es siempre perfecta.
ATENCIÓN: Es importante tener en cuenta que un coeficiente de correlación de 0 entre dos variables, es decir, la ausencia de correlación implica que hay ausencia de correlación lineal pero no quiere decir que no exista ningún tipo de relación entre las variables. De hecho, r podría ser 0 pero podría existir una relación no lineal entre las variables.
Por tanto, sólo si la estructura de la hipótesis sustantiva supone una relación lineal, tendrá sentido emplear el coeficiente de correlación de Pearson. Y es por ello que yo hice hincapié al principio del curso en observar las distribuciones de las variables de cara a normalizarlas antes de proponer una relación entre dos de ellas. Recuerda el caso del PIB per cápita. Su relación casi nunca es lineal con ninguna otra variable cuantitativa porque su distribución es muy poco normal. Pero tras una transformación logarítmica, se puede observar una relación lineal (con un coeficiente de correlación asociado) entre la variable transformada y otra. Asimismo, si el coeficiente de correlación calculado para la distribución conjunta de ambas variables es cercano a cero o cero, deberá tenerse muy presente que la conclusión es que no hay relación lineal. Pero no necesariamente que no exista relación entre las variables.
En Stata obtener una matriz de correlaciones es tan sencillo como usar el comando corr seguido de las variables que queremos cruzar. Recordemos la matriz de correlación de la semana pasada:
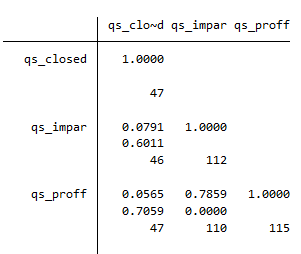
corr qs_closed qs_impar qs_proff
Resultado:
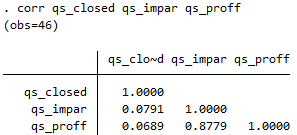
Los números de la matriz son los coeficientes de correlación de Pearson para cada par de variables. Vemos, por ejemplo que qs_proff y qs_impar tienen un coeficiente de correlación muy alto y positivo (cercano a 1), mientras que qs_proff y qs_closed muestran un coeficiente de correlación positivo pero muy cercano a 0, es decir, una correlación muy débil. Para ver esto gráficamente podemos usar el comando twoway combinado con lfit. Así obtendremos la nube de puntos y la recta de ajuste lineal, esto es, la recta que pasa más cerca de todos los puntos a la vez de entre todas las infinitas posibles rectas representables en ese espacio bidimensional.
twoway (scatter qs_proff qs_impar) (lfit qs_proff qs_impar)
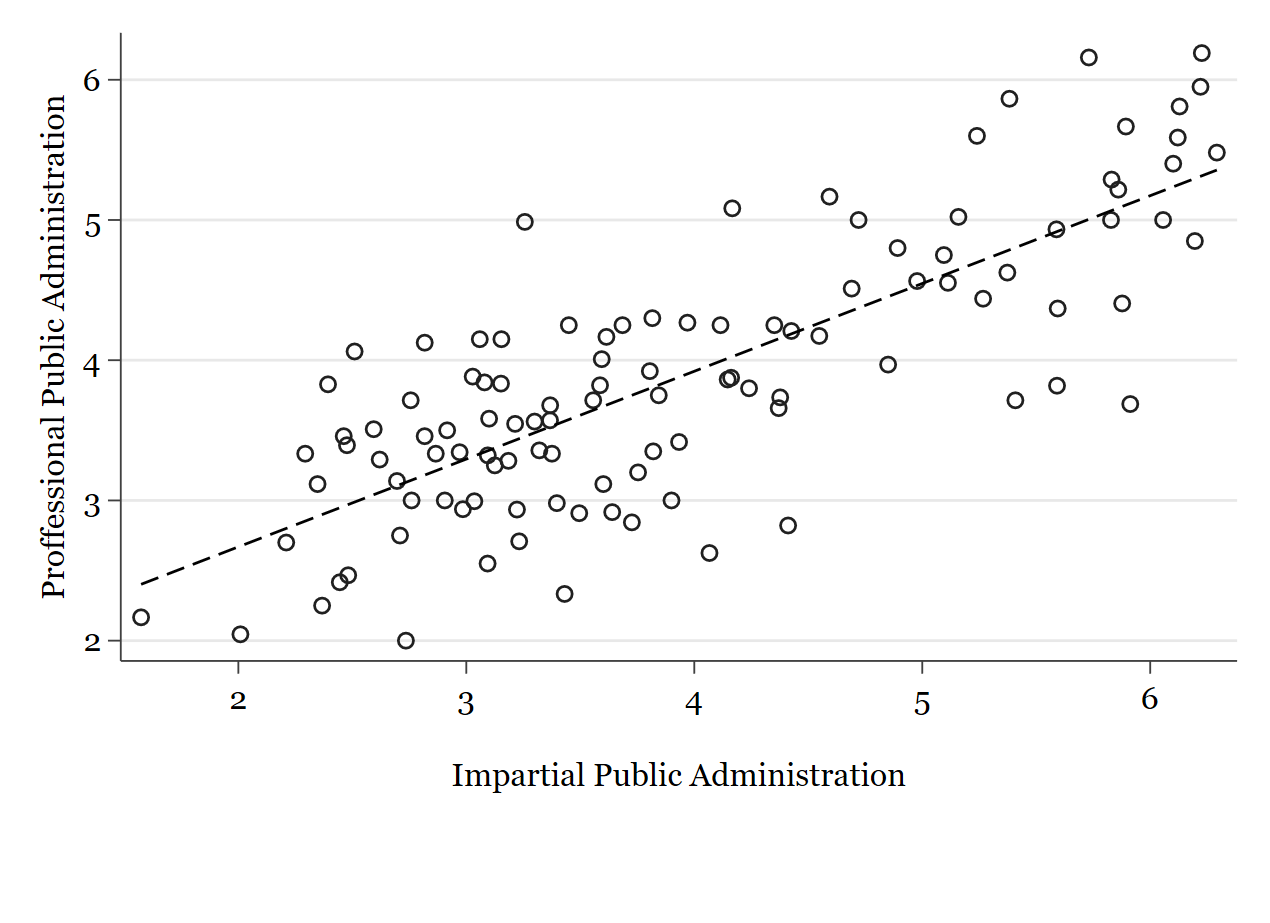
Vemos que, en efecto, los puntos se concentran mucho alrededor de la linea de ajuste.
twoway (scatter qs_proff qs_closed) (lfit qs_proff qs_closed)
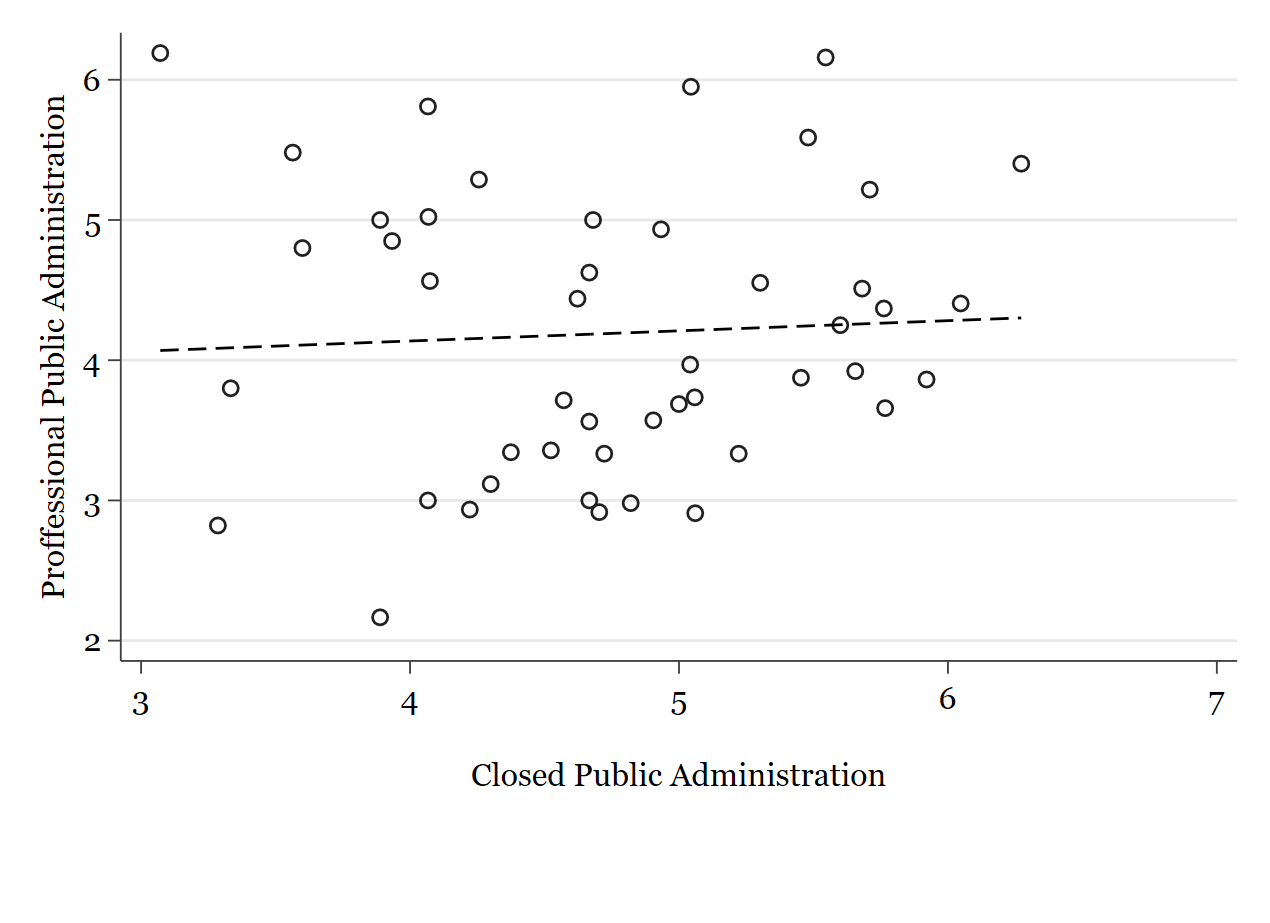
Sin embargo, en este caso vemos que los puntos están mucho más dispersos y, por tanto, la línea tiene una pendiente menos pronunciada, es prácticamente horizontal.
Si ademas de los coeficientes de correlación queremos ver una medida de la significación de este coeficiente, es decir, cómo de significativa estadísticamente es esta relación, usamos la opción sig. También podemos ver el número de observaciones en cada cruce con la opción obs:
pwcorr qs_closed qs_impar qs_proff, obs sig
Resultado:
Para terminar, cabe comentar una de las más famosas frases de las ciencias sociales:
“Correlación no implica causalidad”
–Cualquier científico social en algún momento de su vida
Esta frase es archirepetida en ciencias sociales porque cuando uno empieza a estudiar el concepto de correlación tiende a confundir éste con la causalidad de las relaciones entre variables. Es decir, cuando uno encuentra una relación lineal entre dos variables, esto es, una correlación, tiende a creer que una variable es, automáticamente, la causa de la otra. Es decir, que la variable independiente causa la dependiente. Sin embargo, siento decirte que esto no es así en general y, de hecho, rara vez se puede asegurar que sea el caso. La causalidad es algo muy complejo ya desde la grecia clásica. Aristóteles fue el primer cura o, en otras palabras, el inventor de la religión y a la vez del ateísmo. Precisamente en su estudio de la causalidad propuso el famoso “motor inmóvil” como la causa incausada, el principio de todas las demás relaciones causadas del universo, inventando así el Dios de los filósofos. Este interés por la causalidad que, como se ve, está con nosotros desde los principios de la filosofía y pensamiento occidentales, se exacerbó con los empiristas ingleses (Hume, Bacon…) y llega hasta nuestros días. Pues bien, la ciencia no es un conocimiento mucho más seguro en este sentido. Por mucho método científico que apliquemos y por muchas pruebas estadísticas que usemos, abordar el problema de la causalidad no es para nada trivial. Así que, nunca confundas la correlación con la causalidad. La primera se da simplemente por el hecho de que dos variables se “muevan a la vez” o de una manera sincronizada, mientras que la segunda es ontológicamente mucho más difícil de comprobar. Existen formas, técnicas y procedimientos matemáticos y lógicos que sirven para tratar de discutir si la relación entre dos variables es causal o no, pero en este nivel, lo máximo que puedo pedirte es que busques relaciones entre variables, pero no necesariamente relaciones causales. Para ilustrar esto que digo, échale un ojo al siguiente vídeo y al siguiente sitio web:
Correlación no implica causalidad
En la próxima sesión veremos, por fin, el modelo de regresión lineal simple. Hasta entonces.