Bienvenido/a una semana más. Por fin vamos a ver la última herramienta útil para el contraste de hipótesis de este curso, la regresión lineal. Hasta ahora hemos visto que se pueden formular hipótesis de muchos tipos y que en función del tipo de variables involucradas en dicha hipótesis, se pueden usar contrastes como la prueba T (T-Test), el análisis de varianza (ANOVA), y otros estadísticos en tablas de contingencia (crosstab). Pero nos falta el modelo más famoso y más utilizado cuando se trata de medir la relación entre dos variables y la fuerza de esta: el modelo de Regresión Lineal Simple.
La línea de mejor ajuste
Para empezar a hablar sobre la regresión lineal, debemos comenzar a hablar de la línea de mejor ajuste. Imagina que tienes unos datos con dos variables numéricas continuas. Si representas estos datos, aparece una nube de puntos (diagrama de dispersión) ya que cada observación tiene un valor para cada una de tus variables. Estos dos valores son las coordenadas de estos puntos representados en el plano XY (recuerda lo que vimos la sesión pasada sobre covarianza y correlación). Pues bien, si tratamos de representar una línea que pase lo más cerca posible de todos los puntos a la vez, estaremos representando la línea de mejor ajuste. Se llama de mejor ajuste porque es la recta que mejor se ajusta a la distribución de los puntos, minimizando la distancia a ellos (a todos a la vez). Sin embargo, hay varias formas de minimizar la distancia a los puntos. En cualquier caso, esta recta se denomina recta de regresión y puede ser negativa (decreciente) o positiva (creciente).
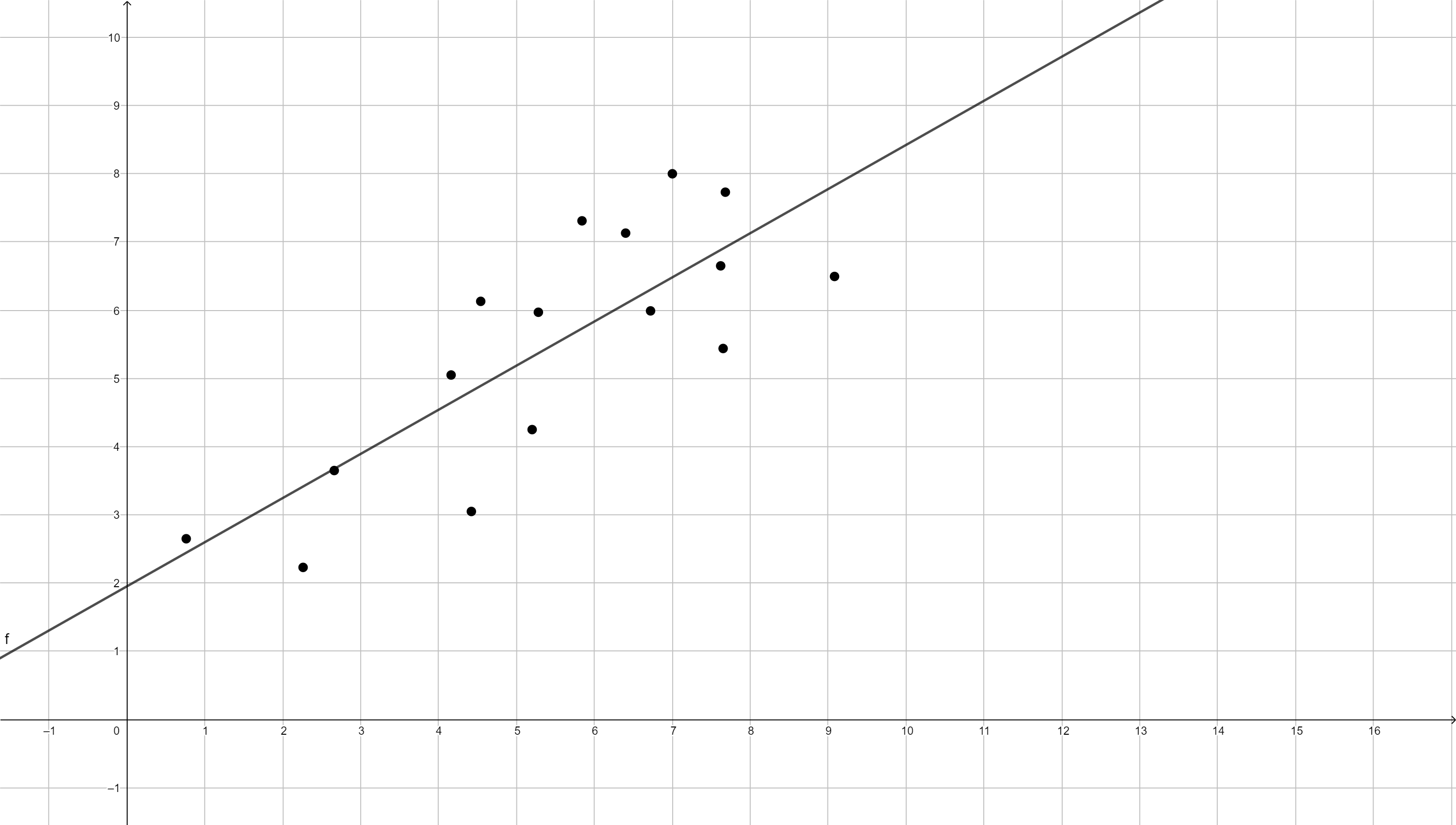
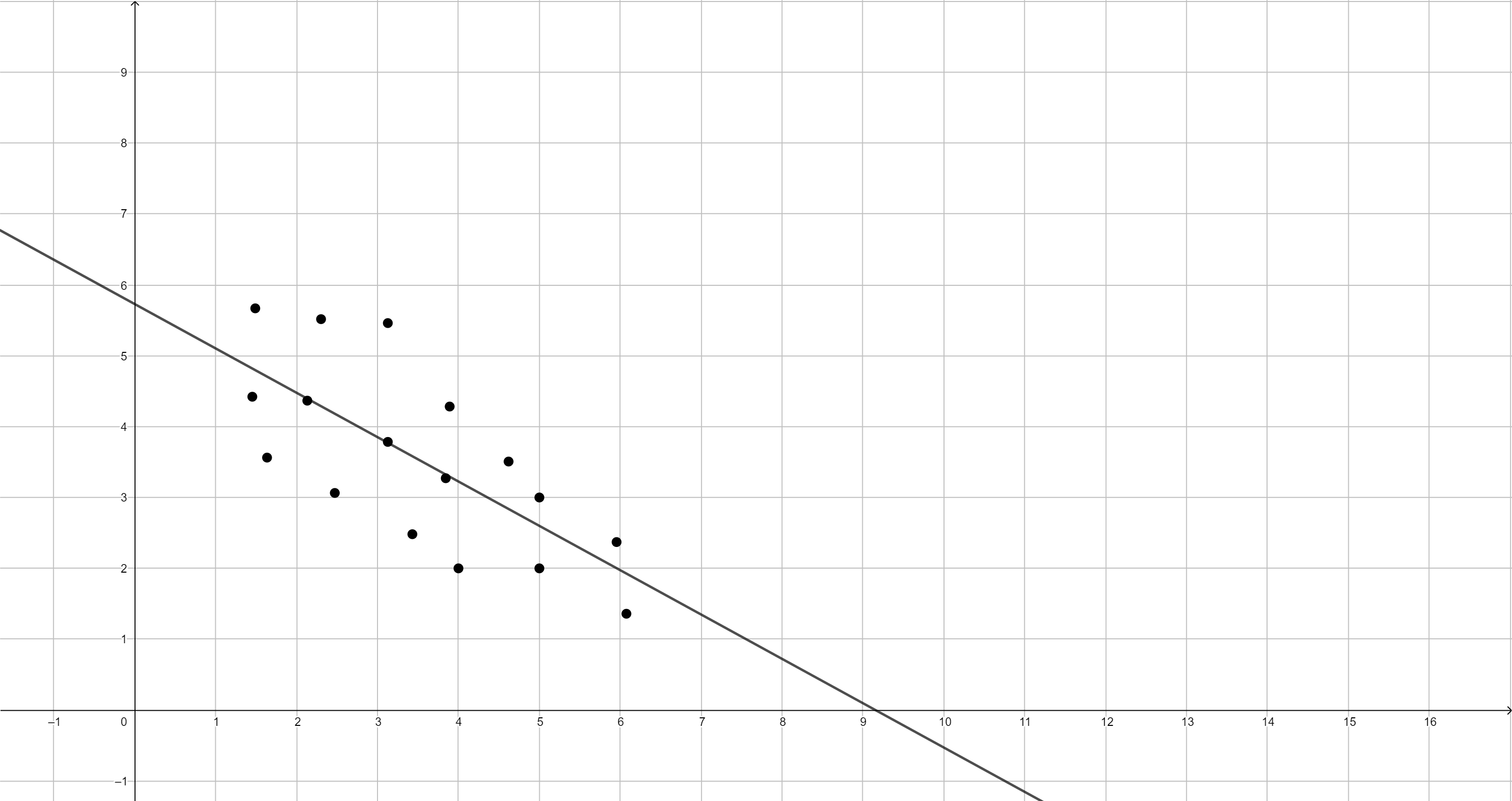
Los puntos representados son los valores de las variables dependiente e independiente, siempre se representa la variable dependiente (o explicada) en el eje y mientras que la independiente (o explicativa) se representa en el eje x:
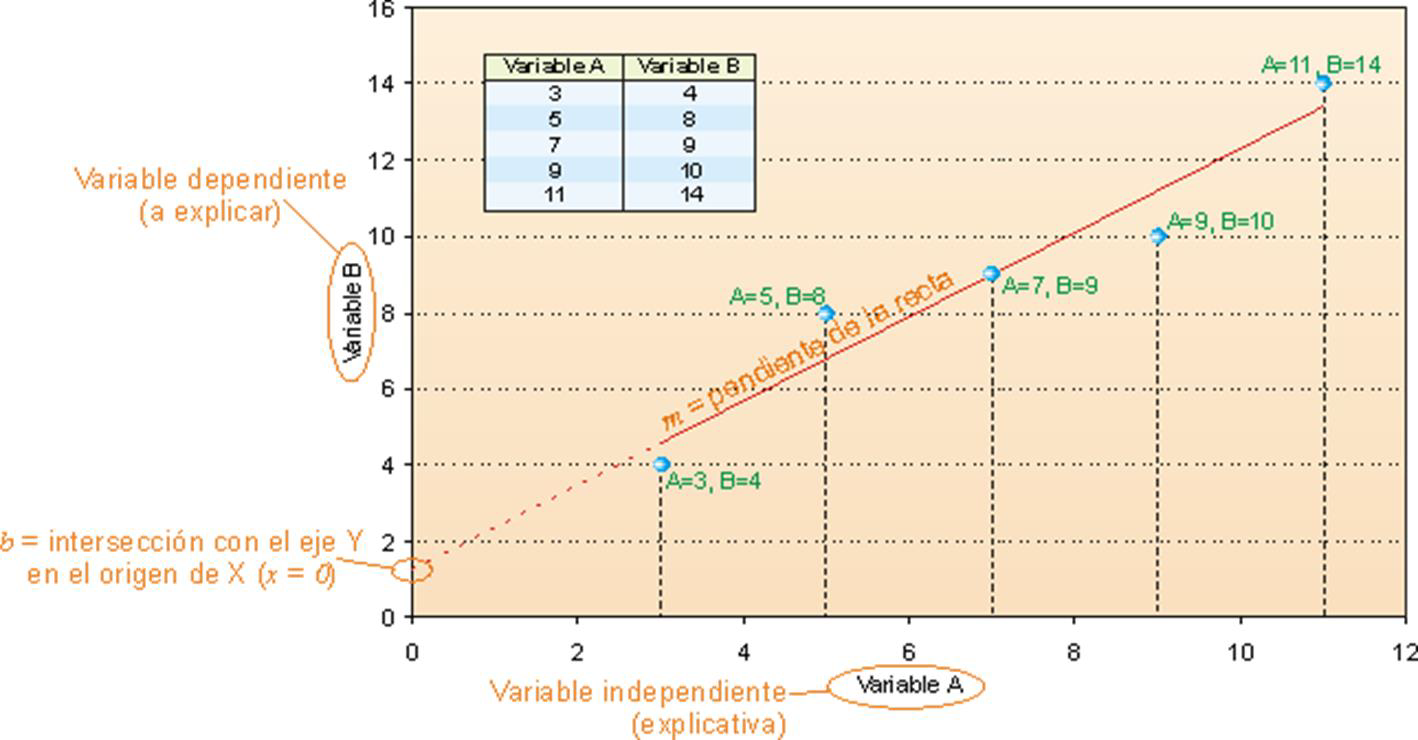
¿Por qué usar una recta?
Bien, partimos de la asunción de que existe una proporción entre la diferencia entre dos valores de la variable X y dos valores de la variable Y. A este factor de proporción entre ambas series se le puede llamar pendiente de la recta y, obviamente, se asume que es constante a lo largo de toda la recta. Si recuerdas de las matemáticas del instituto, una recta puede representarse con dos puntos y las coordenadas de estos puntos pueden usarse para calcular la pendiente de la que hablábamos. En matemáticas, esta es la ecuación general de la recta:
\[y=mx+n\]Pues bien, si ahora tomamos dos puntos con coordenadas \(x_1,y_1\) y \(x_2,y_2\), tenemos la denominada ecuación punto-pendiente:
\[(y_2-y_1) = m\cdot(x_2-x_1) + n\]Despejando llegamos a la pendiente de la recta, que va a ser esencial en este modelo:
\[m = \frac{\Delta{y}}{\Delta{x}} =\frac{y_2-y_1}{x_2-x_1}\]La pendiente representa la inclinación de la recta, o dicho de otro modo, el cambio que se produce en la variable dependiente cuando en la independiente se produce el aumento de una unidad
Finalmente, la \(n\) representa el punto de corte de la recta con el eje y (cuando \(x=0\)). Se denomina ordenada en el origen, constante de la regresión o intercepto.
En estadística, se suelen sustituir los parámetros de la recta (m y n) por la letra b o la letra griega \(\beta\) con subíndices (ej. \(b_0\)). Además, ya que la representación es la de los puntos que existen en la base de datos para dos variables determinadas, se suelen denotar como \(y_i\) y \(x_i\) las variables. Sin embargo, dado que \(y\) es una estimación basada en los valores de x, se denota como \(\hat{y}\) para distinguirla de la \(y\) teórica. Esto es sólo una cuestión de notación. Enseguida veremos el modelo como tal. Pero para que te vayas familiarizando, normalmente representamos la recta con la siguiente notación:
\[\hat{y_i}=b_o+b_1x_i\]Sabiendo que para representar una recta necesitas dos parámetros, te habrás dado cuenta de que podrías obtener infinitas rectas cambiando estos dos valores.
En una nube de puntos es posible trazar muchas rectas diferentes, sin embargo, no todas se ajustan igual de bien a dicha nube de puntos. Por eso, como decíamos, se trata de encontrar la recta capaz de convertirse en la mejor representante del conjunto total de puntos, es decir, la regresión simple consiste en buscar una línea que pase lo más cerca posible de los puntos que reflejan la distribución conjunta de dos variables (Pinta, 2020).
Fíjate en la representación de arriba, verás que la recta se ajusta “lo mejor posible”, pero no pasa por todos los puntos. Unos puntos se alejan más de la recta, otros menos. Pues bien, esta distancia entre la altura del punto (empírica) y la altura de la recta en ese lugar, se denomina residuo. El residuo no es más que el “error” que se comete en cada punto al trazar una recta que trata de ajustar a la nube de puntos. Como decíamos, unos puntos tienen mas distancia a la recta que otros, luego no todos los residuos son iguales. Precisamente, el objetivo del modelo de regresión lineal es minimizar estas distancias, es decir, el tamaño de los residuos. Pero hay varias maneras de hacer esto. Uno podría pensar en medir la distancia de la recta al punto (el residuo) como una distancia geométrica. Recuerda que el residuo (\(e_i\)) es la diferencia entre la altura del punto (\(y_i\)) y la altura de la recta en ese valor de x, es decir \(\hat{y_i}\):
\[e_i = y_i-\hat{y_i}\]Aquí encontramos el primer problema, unos residuos serán positivos (porque los puntos quedarán por encima de la recta de regresión) y otros serán negativos (quedarán por debajo de la recta). Para evitar esto podríamos pensar en medir la distancia como tal, es decir, en usar el valor absoluto de la diferencia (evitando así los signos negativos):
\[e_i = |y_i-\hat{y_i}|\]Esto sería correcto matemáticamente, sin embargo, no es el criterio que se usa en el modelo de regresión lineal. Recuerda que tampoco se calcula así, por ejemplo, la varianza (a pesar de que ésta representa el valor medio de una distancia). Si recuerdas la fórmula de la varianza, se usa la distancia elevada al cuadrado, que también nos evita el problema de los signos negativos. Pues bien, en este modelo, también medimos así los residuos. Por tanto, el método que se suele utilizar para el cálculo de la recta de regresión se denomina Método de Mínimos Cuadrados (OLS en inglés). Se trata por tanto de minimizar la suma de los cuadrados de los residuos, es decir:
\[\min\sum_{i=1}^n(y_i-\hat{y_i})^2 = \min\sum_{i=1}^ne_i^2\]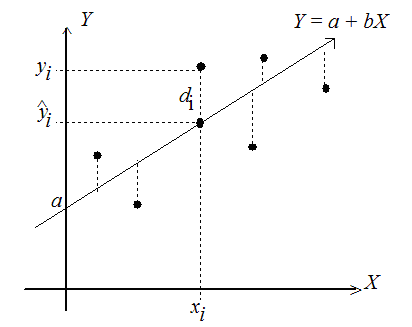
El modelo de Regresión Lineal Simple
El objetivo de los modelos de regresión es explicar el valor de Y en función de una o varias variables independientes o explicativas (X). Al fin y al cabo, se trata de estudiar la dependencia de una variable con respecto a otra o a otras. En este curso no veremos el caso en el que tenemos varias variables independientes afectando a la dependiente, por eso nos limitamos al caso de la regresión lineal simple, pero existe la posibilidad de usar más de una variable independiente para explicar la dependiente. Este modelo se denomina de regresión lineal múltiple. Además, es importante recordar que la variable Y en estos modelos es cuantitativa. No tendría sentido hablar de una variable categórica, por ejemplo, como variable respuesta, explicada, o dependiente. Esos modelos tampoco podremos verlos en este curso, pero se denominan modelos de regresión no lienal (ej. logit, probit, etc.).
Hechas estas aclaraciones, adentrémonos en el modelo de regresión lineal simple. Dada una variable dependiente y una variable independiente, la regresión lineal consiste en obtener una función de la variable independiente que permita explicar el valor de la dependiente. A partir de una muestra de n observaciones de las variables, se trata de aproximar los valores de Y, la variable dependiente, mediante una función de la variable X, variable independiente, que exprese la asociación entre Y y X. (Pinta 2020) El modelo puede expresarse matemáticamente así:
\[y=\beta_0 + \beta_1x+\epsilon\]donde \(y\) es la variable dependiente, \(x\) la variable independiente, \(\beta_0\) es el intercepto y \(\beta_1\) la pendiente de la recta de regresión o, más concretamente, cuánto cambio se produce en \(y\) por cada unidad de incremento en \(x\). Se trata, por tanto, de un indicador de la relevancia del efecto que los cambios en \(x\) tienen sobre \(y\).
Por otro lado, \(\epsilon\) es el término de error. Representa los factores que influyen en \(y\) además de la propia variable \(x\). Es decir, el componente aleatorio de \(y\) que no viene explicado por \(\beta_0+\beta_1x\). En un modelo de regresión, siempre es necesario introducir este término de error, que incluye: los comportamientos puramente aleatorios, el efecto de otras variables independientes no incluídas en el modelo pero que deberían ser incluídas, las imperfecciones en la medición empírica de las variables, los errores derivados de la forma funcional elegida, etc. (Guillen, 1992:17; Molina y Rodrigo, 2009)
El valor que más nos interesa a nosotros de cara a interpretar los cálculos que enseguida veremos en Stata, es la pendiente (\(\beta_1\)). Este coeficiente puede tomar valores negativos y positivos siendo mayores en valor absoluto cuando mayor sea la pendiente de la recta de regresión.
- Si la relación entre \(x\) e \(y\) es positiva, \(\beta_1>0\), es decir, cada incremento de una unidad en \(x\), producirá un incremento en \(\hat{y}\) igual a \(\beta_1\).
- Si la relación entre \(x\) e \(y\) es negativa, \(\beta_1<0\), es decir, cada incremento de una unidad en \(x\), producirá un decremento en \(\hat{y}\) igual a \(\beta_1\).
- Finalmente, \(\beta_1\) puede ser 0 si la recta de regresión fuese horizontal, es decir, si no existiera relación lineal entre \(x\) e \(y\).
En resumen:
El modelo de regresión lineal simple es una técnica estadística que permite estudiar la relación entre una variable dependiente (VD) y una variable independiente (VI). Tiene dos objetivos principales:
- Averiguar en que medida la VD puede estar explicada por la VI
- Obtener predicciones en la VD a partir de la VI
Como hemos visto, el procedimiento implica obtener la recta que minimiza la distancia a la nube de puntos que representa la distribución conjunta de las variables. Esto se consigue mediante el procedimiento de mínimos cuadrados.
Un ejemplo, el modelo de Regresión Lineal Simple en Stata
Vamos a analizar la posible relación entre la esperanza de vida en un país y el nivel de corrupción. Fíjate antes de empezar en que ambas variables son cuantitativas continuas. En la base de datos de Quality of Government encontramos las siguientes dos variables wdi_lifexp y ti_cpi.
Lo primero que podríamos hacer es un diagrama de dispersión para ver cómo se relacionan entre sí estas variables (sólo para tener una idea).
// Recuerda, variable dependiente primero, independiente después: twoway (scatter wdi_lifexp ti_cpi)
Resultado:
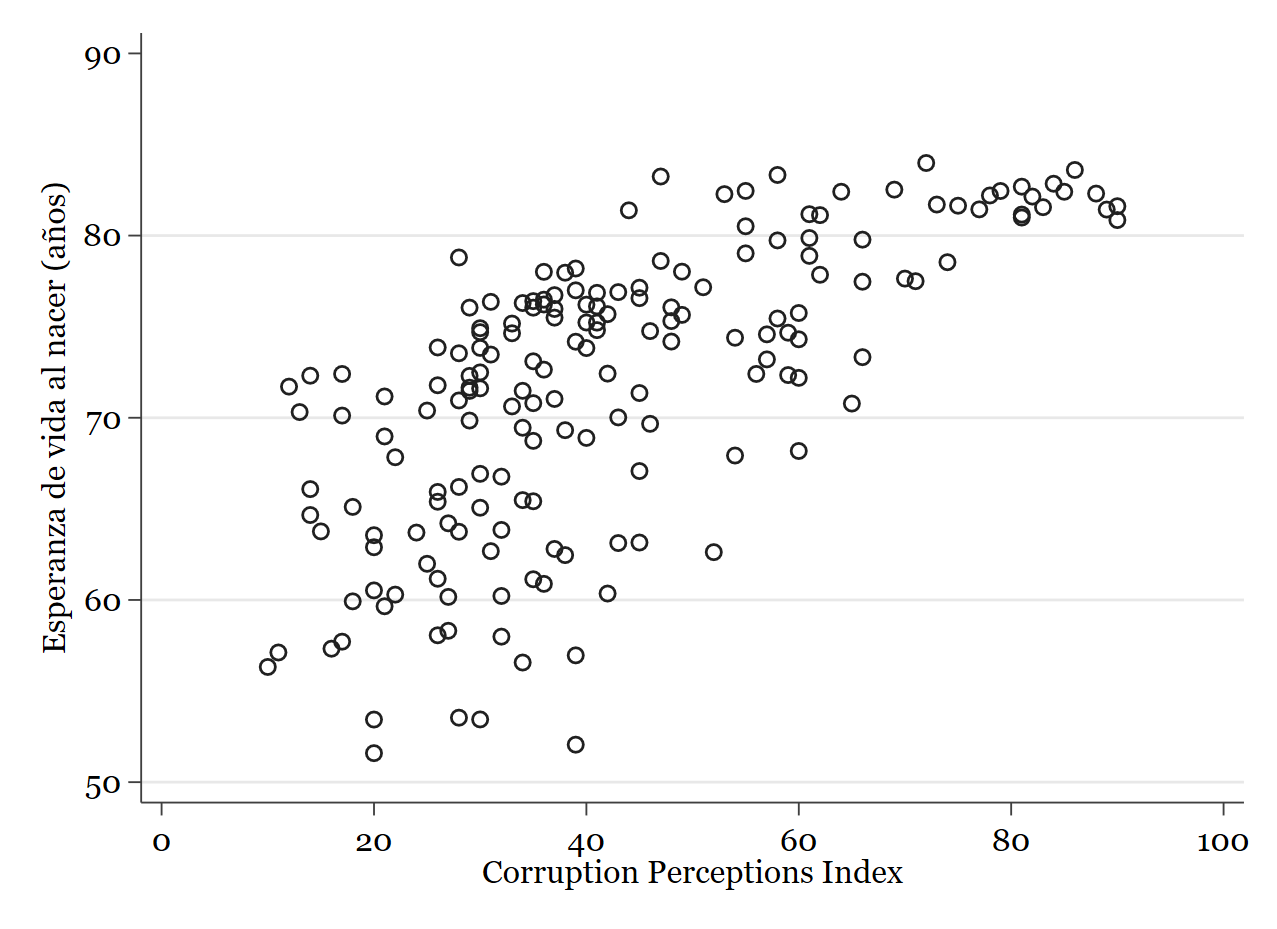
Un momento, qué extraño, ¿cuanta más corrupción mayor esperanza de vida?
CUIDADO: asegúrate siempre de saber qué miden y cómo lo miden tus variables. La variable de percepción de la corrupción está ordenada “al revés” de como nosotros queremos interpretarla.
Para saber cómo está codificada una variable, hay que visitar el codebook. En particular, la variable ti_cpi de acuerdo con QoG toma valores pequeños (cercanos a 0) para niveles altos de corrupción:
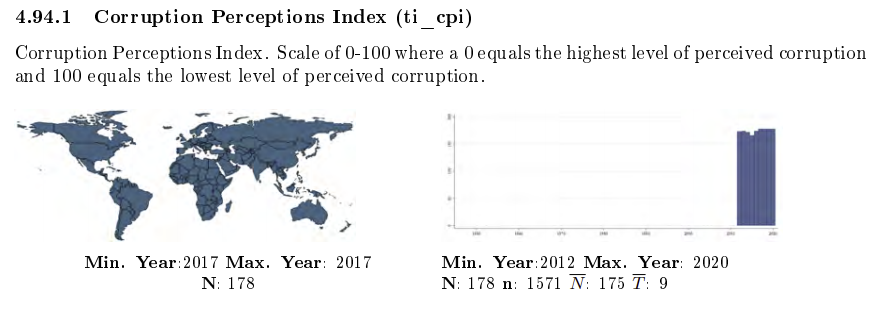
Entonces debemos invertir primero esta variable para que mida lo que nosotros queremos:
// Invertimos la variable de corrupción. Como va de 0 a 100 podemos hacer lo siguiente: gen ti_cpiinv = 100 - ti_cpi // Si volvemos a pedir el diagrama de dispersión: twoway (scatter wdi_lifexp ti_cpiinv)
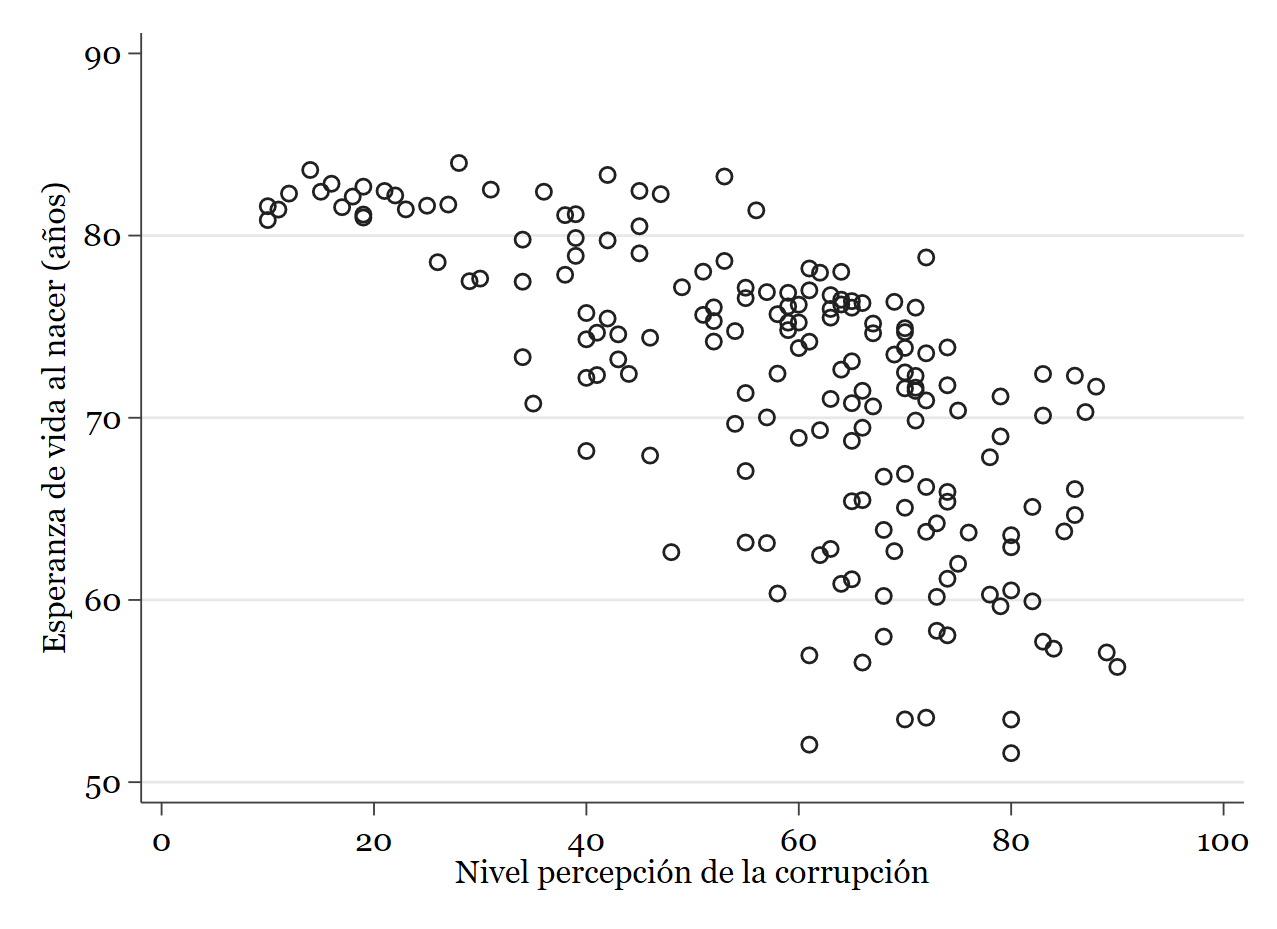
Parece a simple vista que existe una relación más o menos lineal y negativa entre las variables. Veamos qué dice el modelo de regresión lienal:
regress wdi_lifexp ti_cpiinv
Salida:
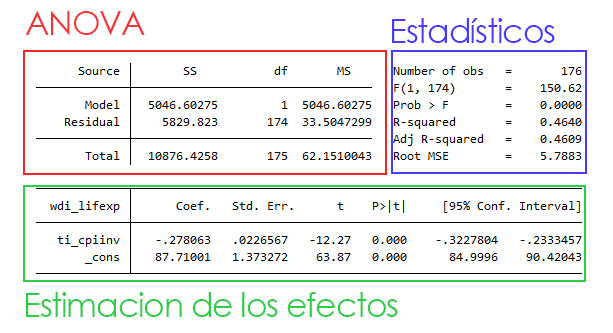
Como puedes ver en la salida volvemos a tener un Análisis de la varianza (ANOVA). Ademas, tenemos todos los estadísticos del modelo (nos fijaremos principalmente en dos de ellos) y debajo la estimación de los resultados. Empezando por el ANOVA, vemos que es idéntico al que vimos la semana pasada para variables categóricas. nos sirve para calcular el estadístico F que aparece a la derecha. Este estadístico (y su p-value asociado) nos informa de que existe una relación entre los valores de x y los valores de y, es decir, que en media, los valores de y cambian según lo hacen los de x. A continuación en los estadísticos nos encontramos el \(R^2\) (R-squared) y el Adj R-squared. Nos fijaremos siempre en el segundo, pues es una corrección algo más conservadora del primero. Este estadístico nos informa de que somos capaces de explicar un 46% de la variabilidad de y con la variable explicativa x. Fíjate que sólo hemos introducido una variable explicativa. Quizás con más variables habríamos sido capaces de explicar un porcentaje mayor. Finalmente, tenemos el root MSE (root mean squared error en inglés). Este estadístico nos da una medida de la desviación de las predicciones. Cuanto menor es, mejores son los pronósticos o, dicho de otro modo, mejor se ajusta la recta a la nube de puntos. Pero antes de seguir, ¿cómo se calculan estos estadísticos?
La bondad del ajuste
Todos estos estadísticos nos hablan de la bondad del ajuste, es decir, de cómo de bien se ajusta la recta de regresión a los datos. Para medir esta bondad del ajuste se usan principalmente dos medidas:
- Una absoluta: el error típico de la regresión o desviación típica de los residuales (root MSE).
\(S_e = \sqrt{\frac{\sum_{i=1}^ne_i^2}{n-k}} = \sqrt{\frac{\sum_{i=1}^n(y_i-\hat{y_i})^2}{n-k}}\)
- Una relativa: el coeficiente de determinación \(R^2\).
El problema de la primera medida es que no está acotada superiormente y depende de las unidades de la variable dependiente. Para corregir esto, se usa el \(R^2\).
Para entender el coeficiente de determinación debemos echar un ojo a la tabla del ANOVA. Pues \(R^2\) se obtiene como el cociente de dos sumas cuadráticas, a saber, la correspondiente a la regresión y la correspondiente a la variable dependiente (Escobar et al., 2009:284). Es decir, representa la proporción de varianza de y explicada por las variables implicadas en el modelo de regresión ajustado a los datos (x en el modelo de regresión lineal simple)(Molina y Rodrigo, 2009).
\[R^2 = \frac{SCReg}{SCT}\]A su vez, recuerda que las sumas cuadráticas implicadas pueden obtenerse de la siguiente manera:
\[SCT = \sum_{i=1}^n(y_i-\hat{y_i})^2\] \[SCReg = \sum_{i=1}^n(\hat{y_i}-\bar{y})^2\] \[SCRes = \sum_{i=1}^n(y_i-\hat{y_i})^2\]El Coeficiente de Determinación es adimensional y oscila entre 0 (sin ajuste) y 1 (ajuste perfecto). Es decir, si todos los valores empíricos (los puntos) se situaran sobre la recta del modelo, el valor de \(R^2\) sería 1. Como hemos dicho, este estadístico indica la proporción de la variable dependiente explicada por la/s variable/s independiente/s. Es decir, explica el porcentaje de la varianza de la variable dependiente que es explicado por el conjunto de las independientes.
Este coeficiente es muy útil y su interpretación es muy intuitiva. Sin embargo, tiene un problema importante, cuantas más variables independientes se incluyen en el modelo (sean estas explicativas o no) mayor es su valor. Esto quiere decir que puede engañarnos al indicar un porcentaje de variabilidad de y explicada mayor del que realmente explican nuestras variables independientes. Para solucionar esto, se tiene el \(R^2\) ajustado:
\[R_aj^2 = R^2 - (1-R^2)\frac{k-1}{n-k}\]donde k es el número de parámetros (variables) y n el número de observaciones.
Cuanto mayor es el tamaño muestral, por tanto, más se parecen \(R_aj^2\) y \(R^2\)
Estimación de los efectos
La última parte de la salida de Stata es donde aparecen los valores de las “betas”, tanto el intercepto (\(\beta_0\)) como la pendiente de la recta (\(\beta_1\)). Recuerda que nuestro modelo puede escribirse así:
\[y=\beta_0 + \beta_1x+\epsilon\]wdi_lifexp=\(\beta_0 + \beta_1\cdot\) ti_cpiinv \(+\epsilon\)
Si habías pensado que en el caso de la regresión no se usaba la estadística inferencial, te equivocabas. Por supuesto, nuestro objetivo no es sólo calcular una recta de ajuste a los puntos empíricos de la muestra, sino tratar de inferir resultados de la población de donde se ha extraído dicha muestra. Para esto es necesario hacer un contraste de hipótesis. Pues bien, en el modelo de regresión lineal simple, el contraste de hipótesis debe realizarse sobre los coeficientes de la regresión, es decir, sobre los valores de esta última parte de la salida de Stata. podemos decir que, según los resultados, \(\beta_0\) es \(87.71001\) y \(\beta_1\) es \(-0.278063\). Es decir, que la recta de regresión de la que hablamos es esta:
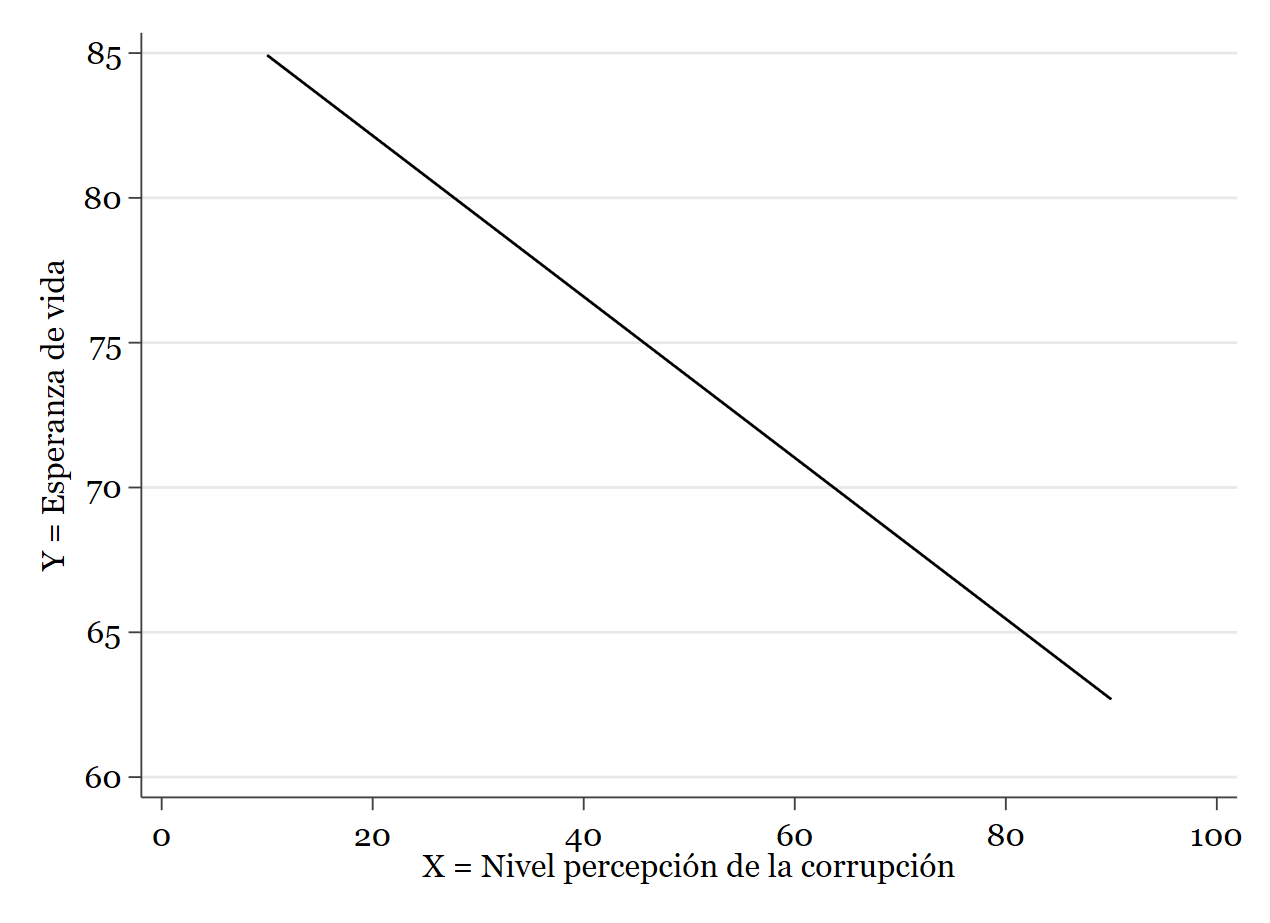
Si quieres superponer la nube de puntos y la línea, ya sabes cómo hacerlo:
twoway (scatter wdi_lifexp ti_cpiinv) (lfit wdi_lifexp ti_cpiinv)
Resultado:
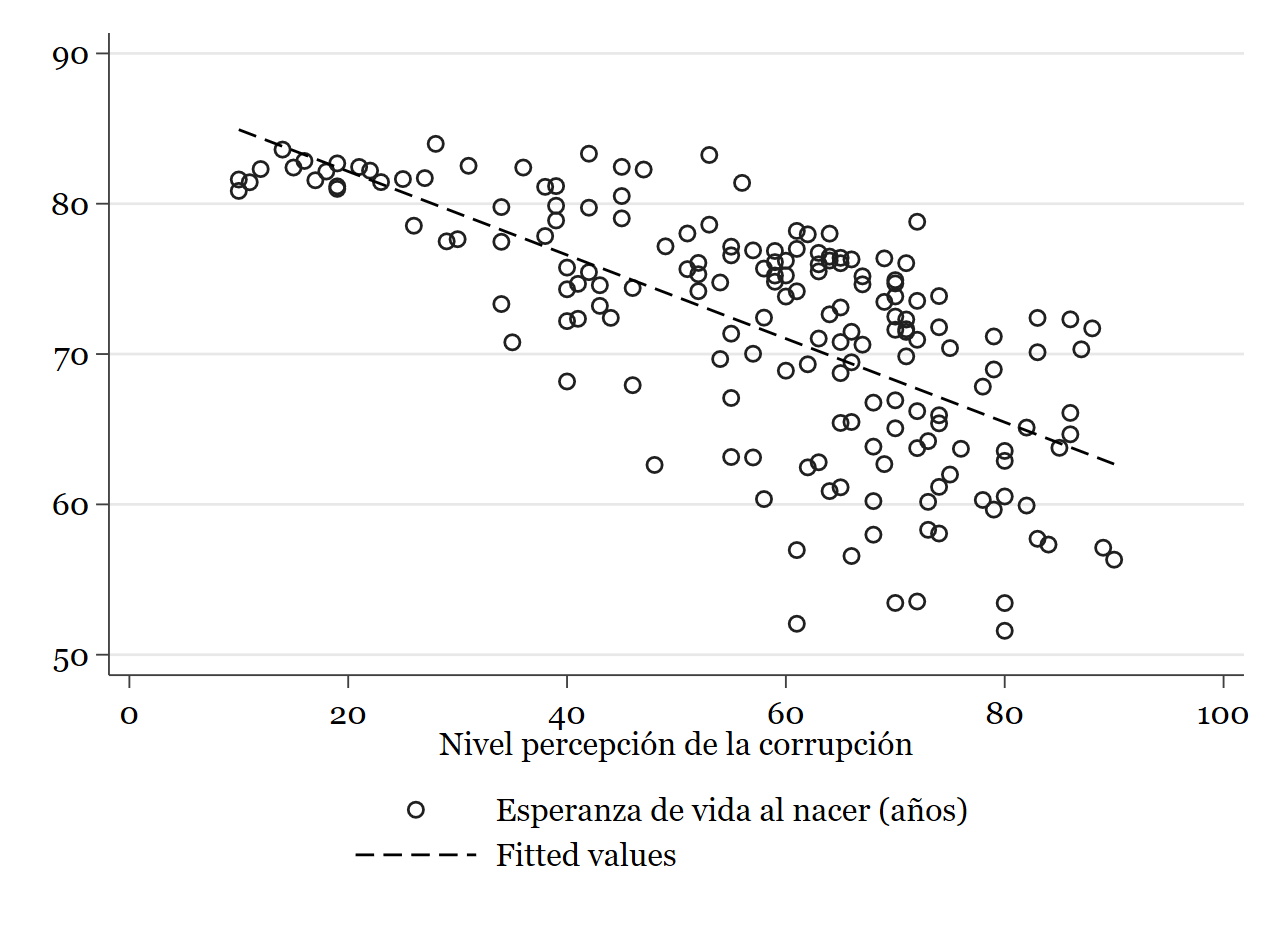
Ahora sólo falta saber si estos valores son estadísticamente significativos, es decir, si se puede asumir que no son debidos al azar. Para eso, es necesario un contraste de hipótesis para cada coeficiente. En la tabla ves además del error estándar, el valor del estadístico T y su p-value asociado. Una vez más, el estadístico T nos ayuda a contrastar la hipótesis nula. En este caso, la hipótesis nula es que el coeficiente es 0 (es decir, que no existe ningún efecto de X sobre Y). Si el valor del estadístico T es grande en valor absoluto (o el p-value pequeño), podremos rechazar la hipótesis nula y concluiremos que el efecto de x sobre y existe y es significativamente distinto de 0. De hecho, el efecto lo mide el propio coeficiente. Recuerda que la interpretación es la siguiente:
por cada unidad que aumenta el índice de percepción de la corrupción la esperanza de vida disminuye 0.278 unidades (en este caso años). Dado que el p-value asociado al coeficiente es prácticamente 0, podemos rechazar la hipótesis nula y concluir que este número, 0.278 es significativamente distinto de 0. Otra forma de contrastar la hipótesis nula es fijarse en la última columna (el intervalo de confianza del coeficiente). Como siempre, la estimación puede ser puntual o por intervalo. El intervalo debe interpretarse de la siguiente manera:
\[b_1 \pm t_c\sigma_{b_1}\]donde \(b_1\) es el coeficiente, \(t_c\) es el valor crítico del estadístico T de Student y \(\sigma_{b_1}\) es el error estándar asociado. Como siempre, Stata se encarga de hacer este cálculo y nos ofrece directamente los valores. Como ves, ambos valores son negativos, lo cual nos indica que el 0 no está contenido en el intervalo, por lo que podemos rechazar la hipótesis nula y concluir que el efecto de x sobre y es significativo.
Supuestos del modelo de regresión lineal simple
Hasta ahora hemos podido comprobar empíricamente que el nivel de corrupción de un país afecta a la esperanza de vida. Hemos contrastado empíricamente que la relación existe y que es negativa, aunque el efecto es pequeño: por cada punto porcentual que aumenta el nivel de corrupción, la esperanza de vida baja 0.27 años. Ahora bien, todo esto podría no haber servido para nada. Recuerda que estamos hablando de un modelo matemático. Modelar la realizad no es una tarea sencilla y el Modelo de Regresión Lineal Simple parte de unos supuestos que no siempre se cumplen. No entraremos en detalles en este nivel, pero es importante tener en cuenta que si uno quiere asegurarse de que sus resultados son válidos, debe comprobar que se cumplen los siguientes supuestos:
Linealidad
Se asume que la función que relaciona las variables del modelo es lineal. El modelo de regresión es lineal en sus parámetros.
Normalidad
El término de perturbación (error) está normalmente distribuido, es decir:
\[\epsilon \sim N(0,\sigma)\]Los residuos siguen una distribución normal, es decir, los residuos observados y los esperados bajo la hipótesis de normalidad han de ser parecidos.
En Stata, podemos pedir una prueba ya conocida de normalidad (el test de Shapiro-Wilk). Se pide usando el comando swilk.
swilk lifexpres
Resultado:
Vemos que no cumplimos este supuesto. El test nos dice que tenemos evidencia suficiente al 95% de confianza para rechazar la hipótesis nula de normalidad, es decir, que la distribución de los residuos no es normal.
Independencia
Este supuesto es básico y consiste en asumir que los residuos son independientes entre sí, es decir, que no se puede predecir el valor de un residuo sabiendo el valor del anterior. También se dice que no existe autocorrelación entre las perturbaciones:
\[Cov(\epsilon_i,\epsilon_j)=0; (i\neq j)\]Para comprobar esto existen muchos tests (como el estadístico Durbin-Watson) pero lo más intuitivo a este nivel es representar gráficamente los residuos y comparar si se observa algún patrón (dependencia) o, por el contrario, los residuos se distribuyen caóticamente en una nube de puntos (independencia). Para hacer la representación gráfica de los residuos en Stata podemos usar el siguiente comando una vez se ha lanzado la regresión:
rvfplot
Resultado:
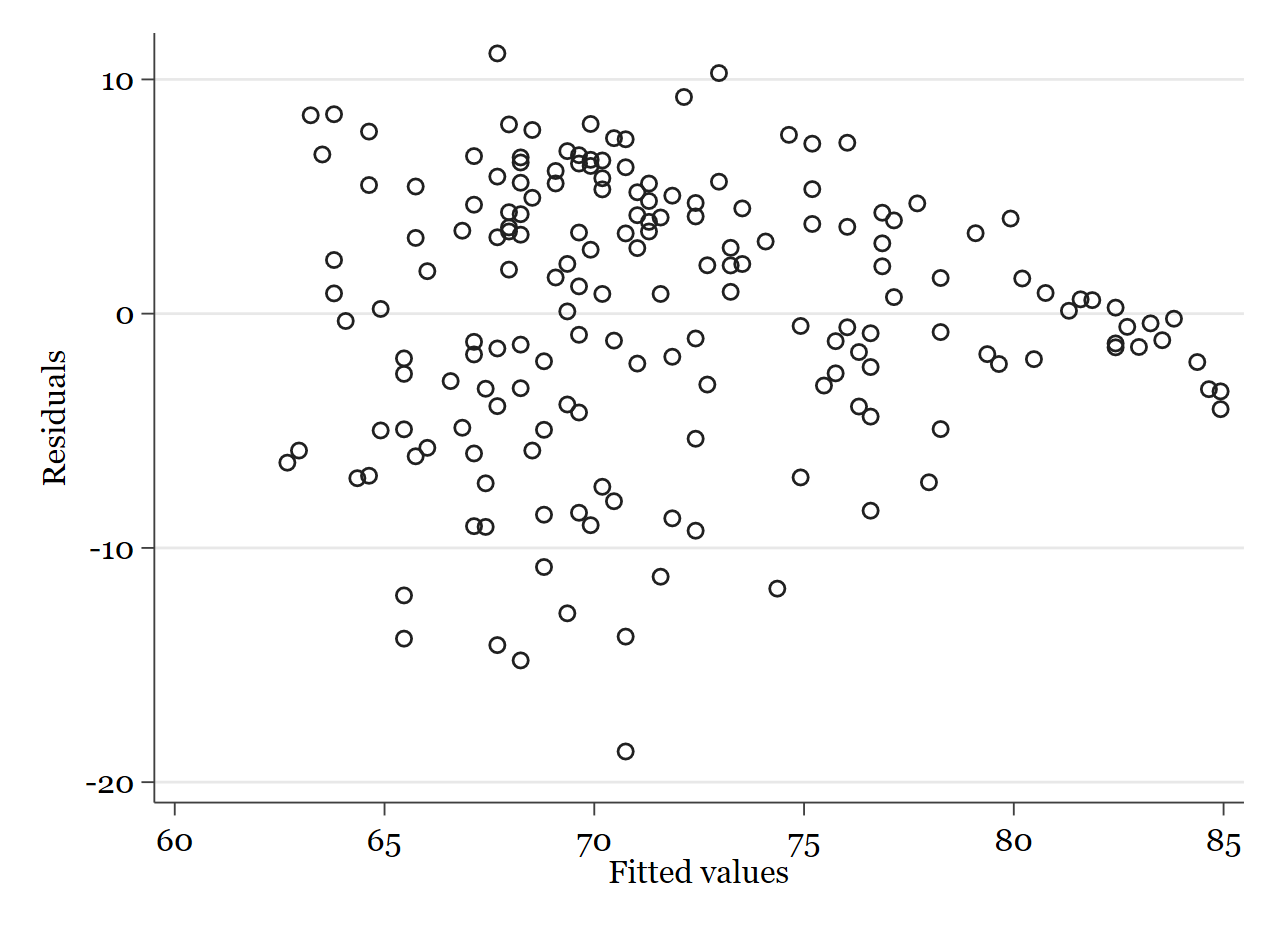{width=”500”}
Como ves, aunque se puede ver cómo se van concentrando en torno a 0 hacia el final, no se observa un patrón claro en los residuos, esto nos indica independencia.
Homocedasticidad
Este supuesto consiste en que para cada conjunto de casos con una \(x_i\) dada, la varianza de los residuos (\(\epsilon\)) es constante u homocedástica. Matemáticamente:
\[\forall x_i \; Var(\epsilon_i=\sigma^2)\]Dicho de otra forma, la varianza del término de error es la misma para todas las observaciones. Las varianzas residuales han de ser las mismas independientemente de los valores de las variables independientes y, por extensión, de los valores predichos de la dependiente (Pinta, 2020).
este supuesto puede comprobarse de dos maneras principalmente: mediante el análisis gráfico, como en el caso de independencia de arriba o usando el test de Breusch-Pagan. Este test en Stata se pide con el comando hettest:
hettest
Resultado:
Tanto mirando el gráfico de arriba como mirando el test, podemos concluir que tampoco cumplimos el supuesto de homocedasticidad. En el gráfico se ve cómo los residuos son menos variables a la derecha y mucho más variables a la izquierda (heterocedasticidad). En el test, rechazamos la hipótesis nula de igualdad de varianza dado que el p-value es muy bajo.
El último supuesto solo aplica al modelo de regresión lineal múltiple, pues tiene que ver con la independencia entre las variables independientes (regresores), como aquí nos ceñimos al modelo de regresión lineal simple, no lo veremos.
Como ves, nuestro análisis parecía correcto. El coeficiente beta asociado al efecto de la variable independiente (corrupción) indicaba un efecto negativo y estadísticamente distinto de 0. Sin embargo, no cumplimos dos de los supuestos más importantes del modelo de regresión lineal: normalidad y homocedasticidad. Para corregir esto, probablemente lo más fácil sería introducir otras variables explicativas. Recuerda que estamos viendo un caso muy simplificado. En la vida real, ninguna regresión con una única variable independiente explica con rigor y confianza los cambios de una variable dependiente. Así que, en este nivel, no te tomes los supuestos como una barrera. Es importante que los conozcas, pero es suficiente con que el valor del coeficiente de la variable explicativa sea significativamente distinto de 0.
Más adelante, si sigues con el análisis de datos o la ciencia social empírica (cuantitativa), verás el modelo de regresión lineal múltiple y verás cómo se puede mejorar nuestro modelo para explicar las diferencias en la esperanza de vida en los países. Hasta entonces, practica con este modelo, entiende los supuestos y prueba distintas relaciones en Stata para familiarizarte con la sintaxis.